¿Qué es la curva característica del test – CCT – en IRT?

.

Por: Cristian Stiven Tarapues Calpa

Bienvenidos a este blog, donde exploraremos un concepto clave de la Teoría de Respuesta al Ítem (IRT): la Curva Característica del Test (CCT). Este concepto, fundamental en la psicometría moderna, nos permite comprender cómo se comporta un test a lo largo del rango de habilidades de los examinados (Hambleton & Swaminathan, 2010).

La Curva Característica del Test (CCT) es una función no lineal que describe la relación entre la habilidad latente de una persona (θ) y la probabilidad de responder correctamente a los ítems del test (Baker, 2001). En esencia, la CCT sintetiza el comportamiento del test a lo largo del continuo de habilidad, mostrando en qué niveles de habilidad 𝜃 aporta más información útil y qué tan precisa es para distinguir entre personas con diferentes niveles de competencia.

¿Por qué es importante?

La forma de esta curva tiene implicaciones directas en la precisión de la medición (confiabilidad), la discriminación entre niveles bajos y altos de la habilidad y la detección de sesgos o deficiencias en el test (De Ayala, 2009)

Ejemplo gráfico
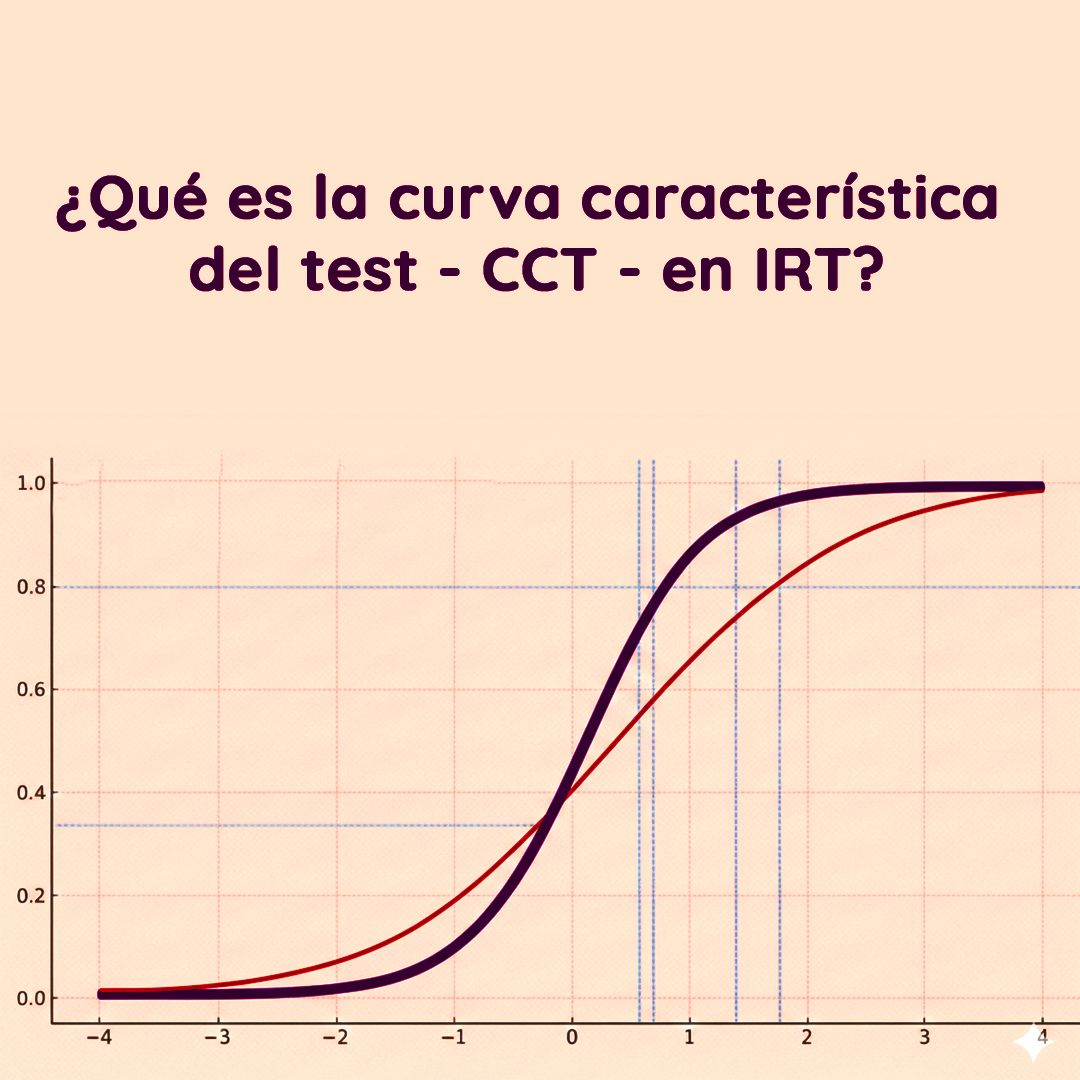
 A continuación, presento una gráfica ilustrativa de una Curva Característica del Test. Esta curva agrega la información de todos los ítems del test en una sola función:

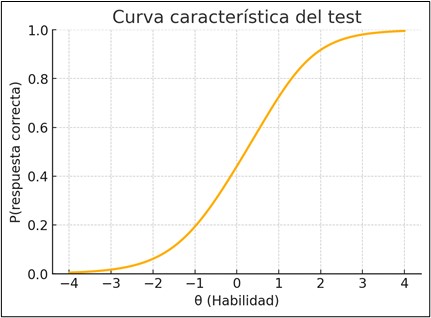
Componentes clave de la CCT

1. Eje horizontal (θ): representa la habilidad latente de los examinados.
   
   
2. Eje vertical: indica la probabilidad de respuesta correcta.
   
   
3. La curva en sí: refleja el desempeño promedio esperado a distintos niveles de habilidad.

FORMA

La Curva Característica del Test (CCT) adopta un perfil sigmoidal o en forma de S, típico en modelos de Teoría de Respuesta al Ítem (IRT). Esta forma se caracteriza por tres zonas:

• Una fase inicial plana, donde la probabilidad de acierto se mantiene baja a pesar de aumentos en la habilidad.
  
  
• Una zona central de transición rápida, donde pequeños cambios en el nivel de habilidad (θ) generan aumentos significativos en la probabilidad de respuesta correcta.
  
  
• Una fase final también plana, donde la probabilidad se estabiliza cerca del valor máximo.
  
  
• Parámetros
• En los modelos logísticos de la Teoría de Respuesta al Ítem (como el modelo de 2 parámetros), la CCT se caracteriza por dos parámetros fundamentales:
• Discriminación: La pendiente de la CCT en su tramo intermedio indica el poder discriminativo del test. Una pendiente empinada sugiere que el test es muy sensible a diferencias sutiles de habilidad: discrimina eficazmente entre personas con niveles similares de habilidad (De Ayala, 2009). Por el contrario, una curva plana implica baja sensibilidad: el test cambia poco su probabilidad de acierto incluso con amplias variaciones en habilidad, lo que indica un bajo poder de discriminación (Hambleton & Swaminathan, 2010).
• Dificultad: El desplazamiento horizontal de la CCT refleja la dificultad promedio del test. Si la curva está desplazada hacia la derecha, se requieren niveles altos de habilidad para alcanzar una probabilidad del 50 % de respuesta correcta, lo que indica un test difícil. Si la curva está hacia la izquierda, el test es más fácil, ya que basta con una menor habilidad para tener éxito (Baker, 2001).

El punto de inflexión de la CCT, donde la pendiente es máxima y la probabilidad esperada de acierto es 0.5, se considera una medida directa de la dificultad del test. Por ejemplo, en la gráfica 1 el punto está cerca de θ=0, lo que indica que el test está calibrado para una población con habilidad media (De Ayala, 2009).

Función matemática

La CCT se expresa como una función que suma las probabilidades de respuesta correcta para todos los ítems del test.

La fórmula de la Curva Característica del Test (CCT) es:

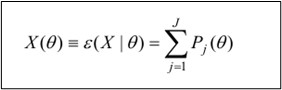
Componentes de la Fórmula:

1. 𝑋(𝜃): Representa la puntuación esperada del test para un nivel específico de habilidad 𝜃. En otras palabras, es la media de las puntuaciones observadas que se espera para un examinando con un nivel de habilidad 𝜃.
2. E(X∣θ): Esta notación denota la esperanza matemática (o valor esperado) de la puntuación total 𝑋 dado un nivel de habilidad 𝜃. Es una forma formal de expresar que estamos calculando la puntuación esperada del test.

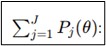
Esta es una suma que va desde 𝑗=1 hasta 𝐽, donde 𝐽 es el número total de ítems en el test. Pj(θ) representa la probabilidad de que un examinando con un nivel de habilidad 𝜃 responda correctamente al ítem 𝑗. Esta probabilidad se obtiene a partir de la Curva Característica del Ítem (CCI) para cada ítem 𝑗.

Desglose y Significado:

• Puntuación Esperada: La fórmula nos dice que la puntuación esperada de un test para un nivel de habilidad específico 𝜃 es la suma de las probabilidades de responder correctamente a cada uno de los ítems del test para ese nivel de habilidad.
• Importancia de Pj(θ): Cada Pj(θ) es derivado de la CCI del ítem 𝑗. Estas probabilidades reflejan cómo cambia la probabilidad de una respuesta correcta en función del nivel de habilidad.
• Suma de Probabilidades: Al sumar estas probabilidades para todos los ítems en el test, obtenemos una puntuación total esperada. Esta suma proporciona una visión general de cómo un examinado con un nivel de habilidad dado podría esperarse que se desempeñe en todo el test, en lugar de solo en ítems individuales.

Relación entre CCI y CCT

El CCI y el CCT están relacionados en IRT (Embretson & Reise, 2000), la CCI representa a nivel de ítem individual las mismas características que el CCT a nivel del test completo. Es decir, la dificultad y discriminación de cada ítem forman parte de los parámetros de dificultad y pendiente del test (Baker, 2001). Así, la CCT es esencialmente una suma de las CCIs individuales (Hambleton et al., 1991).

Por lo tanto, ambos conceptos se complementan para analizar un test. La CCI permite evaluar el funcionamiento de ítems específicos. Luego, la CCT muestra el efecto acumulado de todos los ítems y su interacción con las habilidades latentes (De Ayala, 2009).

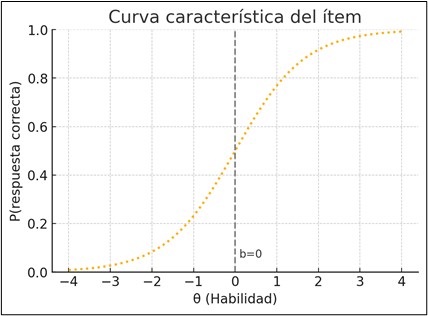
El gráfico 2 anterior muestra un ejemplo concreto de:

• CCI (Curva Característica del Ítem): representada por una línea punteada, corresponde a un ítem con parámetros de discriminación a=1.2 y dificultad b=0. Esta curva describe cómo varía la probabilidad de responder correctamente un ítem en función del nivel de habilidad θ. El punto medio de la CCI (donde la probabilidad = 0.5) coincide con el valor de b, mientras que la pendiente en ese punto refleja su capacidad de discriminación: a mayor a, más empinada la curva, y mayor precisión para distinguir entre examinados con niveles de habilidad cercanos a b.

El gráfico 1 muestra un ejemplo concreto de:

• CCT (Curva Característica del Test): se construye a partir de la combinación de múltiples Curvas Características del Ítem (CCI) y representa la probabilidad esperada de acierto en el test completo a lo largo del continuo de habilidad 𝜃. En este caso, la CCT del grafico 1 resulta del promedio de tres ítems con diferentes niveles de dificultad y discriminación, lo que da lugar a una curva suavemente sigmoidal y centrada cerca de 𝜃=0.2, indicando una dificultad ligeramente superior a la media. La pendiente de la curva es más pronunciada entre θ=−0.5 y θ=1.2, lo que significa que el test es más informativo y preciso en ese intervalo de habilidades. En cambio, en los extremos del continuo, la curva se aplana, reflejando que el test aporta menos información para personas con habilidades muy bajas o muy altas.

Cuando las CCIs incluyen ítems con parámetros inadecuados (por ejemplo, baja discriminación o dificultad mal calibrada), distorsionan la forma de la CCT y reducen la confiabilidad del test (Hambleton & Swaminathan, 2010). Por ello, el análisis conjunto de CCIs y CCT es esencial para evaluar y optimizar la calidad psicométrica de un instrumento de medición.

Para entender en detalle la interpretación de una Curva Característica del Ítem (CCI), te invitamos a ver nuestro blog titulado “¿Qué es la curva característica del ítem – CCI – en IRT?”, donde lo explicamos paso a paso. ¡No te lo pierdas! – Link directo: https://siepsi.com.co/2024/08/31/que-es-la-curva-caracteristica-del-item-cci-en-irt/

¿Cómo sabemos en qué rango un test mide con mayor precisión?

El gráfico 3 responde a esta pregunta al graficar la CCT frente a θ. Fíjate en la pendiente central y en la asíntota en 7 para entender el poder discriminativo y la dificultad global del test.

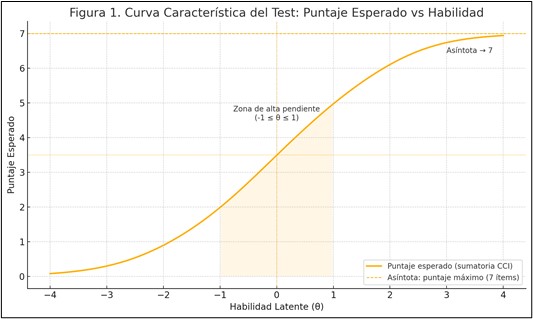
El siguiente gráfico ilustra de un vistazo las propiedades clave de la Curva Característica del Test (CCT) en términos de puntaje esperado (Baker, 2001; Hambleton & Swaminathan, 2010). En él se aprecia que la función es monótona creciente (a mayor θ, mayor puntaje esperado), que tiene una asíntota en 7 (la línea discontinua horizontal marca el máximo puntaje posible, y la curva se aproxima pero nunca lo alcanza; De Ayala, 2009), y que presenta una zona de alta pendiente entre –1 ≤ θ ≤ 1 (área sombreada, donde el test discrimina mejor entre habilidades promedio). Además, la línea vertical punteada en θ = 0 indica que el punto medio del test —y por tanto su dificultad general— está calibrado en un nivel de habilidad moderada (Baker, 2001).

Interpretación:

• La pendiente en la región central refleja la capacidad de diferenciación del test: cuanto más empinada, mejor distingue entre examinados con habilidades cercanas (De Ayala, 2009).
  
  
• La ubicación de la curva en el eje X señala su nivel de dificultad: al estar centrada en θ = 0, rinde mejor midiendo habilidades próximas a esa estimación (Hambleton & Swaminathan, 2010).
  
  

Propiedades fundamentales:

• Monótona creciente: la probabilidad de acierto (y, en consecuencia, el puntaje esperado) aumenta sin retrocesos a medida que crece θ (De Ayala, 2009).
  
  
• Asintótica: se acerca al límite teórico de 7 ítems, pero nunca lo iguala, lo que indica que incluso los examinados de más alta habilidad tienen alguna probabilidad de error (De Ayala, 2009).

Propiedades e Interpretación de la forma de la CCT

La forma de la Curva Característica del Test (CCT) proporciona información valiosa sobre las propiedades psicométricas de un instrumento de medición y su capacidad para evaluar a los examinados a través de diferentes niveles de habilidad. Las características deseables de la CCT incluyen:Alta pendiente para discriminar entre niveles de habilidad: Una CCT con una pendiente empinada indica que el test tiene una alta capacidad de discriminación entre examinados con diferentes niveles de habilidad (Embretson & Reise, 2000). Esto significa que el test puede diferenciar a los examinados que se encuentran en distintos puntos del continuo de habilidad, lo cual es esencial para una medición confiable.

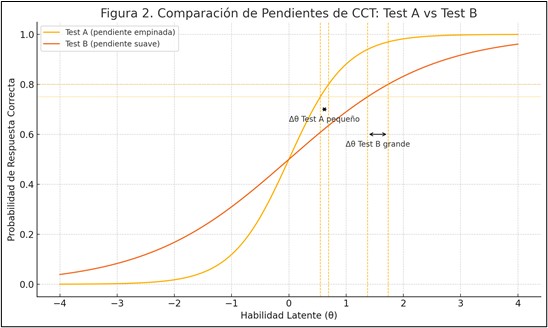
Por ejemplo, imagina dos tests de matemáticas que difieren en la forma de su Curva Característica del Test (CCT). En el gráfico 4 se ilustran dos flechas horizontales que representan los valores de θ correspondientes a probabilidades de 0.75 y 0.80. Cada flecha indica un Δθ, es decir, la cantidad de cambio en la habilidad necesaria para que la probabilidad de respuesta correcta aumente del 75 % al 80 %.

En el Test A, cuya curva presenta una pendiente empinada, el Δθ es pequeño, lo que significa que basta un leve aumento en la habilidad para generar un cambio notable en la probabilidad de acierto. Esto refleja una alta capacidad de discriminación.

En contraste, el Test B, con una pendiente más suave, requiere un Δθ mucho mayor para reflejar ese mismo cambio en probabilidad, lo que indica una menor capacidad de discriminación entre examinados con habilidades similares.

En resumen, el Test A es más preciso para detectar pequeñas diferencias en la habilidad matemática, mientras que el Test B podría no captar con claridad esas variaciones sutiles.

Simetría para cubrir adecuadamente todo el rango de interés: Se busca que la CCT sea simétrica y unimodal, lo que implica que el test cubre de manera uniforme todo el rango de habilidad de interés (Hambleton & Swaminathan, 2010). Una CCT asimétrica o multimodal indica que el test no está midiendo adecuadamente ciertos rangos de habilidad, ya sea porque tiene demasiados ítems fáciles o difíciles, o porque hay problemas con el ajuste del modelo IRT a los datos (De Ayala, 2009).

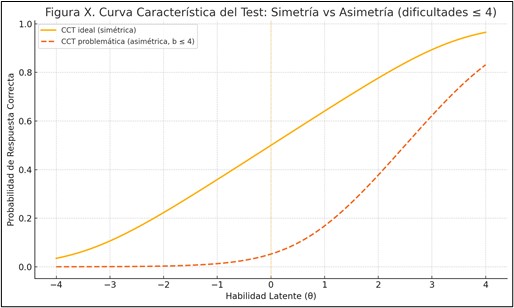
Ejemplo: Consideremos un test de vocabulario en inglés.

CCT ideal (simétrica): ítems con parámetros de dificultad distribuidos uniformemente entre –3 y +3, cubriendo adecuadamente desde principiantes hasta avanzados.

CCT problemática (asimétrica): ítems concentrados hacia el extremo superior (b = 1, 1.5, 2, 2.5, 3, 3.5, 4), lo que deja a los niveles bajos y medios con muy poca información (De Ayala, 2009).

La línea vertical punteada en θ=0 destaca el centro de la escala. Observa cómo la CCT ideal se eleva simétricamente alrededor de ese punto, mientras que la problemática está desplazada y aplanada en la parte izquierda, evidenciando su sesgo hacia habilidades altas (Hambleton & Swaminathan, 2010).

Identificación de rangos de habilidad con baja o alta información: La forma de la CCT permite identificar los rangos de habilidad en los que el test proporciona mayor o menor información psicométrica (Baker, 2001). Los rangos donde la curva es más empinada corresponden a niveles de habilidad con mayor información. Por el contrario, los rangos donde la curva es más plana indican niveles de habilidad con menor información y mayor error de medición.

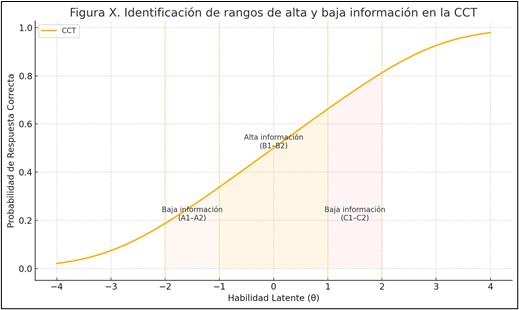
Las líneas verticales punteadas en θ = –2, –1, 1 y 2 delimitan los rangos de competencia del Marco Común Europeo (CEFR):

Se han sombreado tres regiones para destacar la información psicométrica que aporta el test en cada tramo:

2. Zonas de baja información (rosa tenue):  En estos tramos la curva es más plana, por lo que grandes cambios en θ apenas modifican la probabilidad de acierto. El test aporta poca información y el error de medición aumenta.

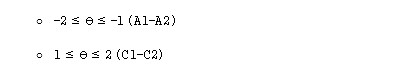
3. Mesetas extremas (θ < –2 y θ > 2): Fuera de los rangos sombreados, la curva se aproxima a 0 o a 1 y prácticamente no sube, indicando que el test es poco útil tanto para medir a principiantes muy básicos (A1) como a muy avanzados (C2).

De este modo, la gráfica facilita la identificación visual de los rangos de habilidad donde el test es más (o menos) informativo, apoyando el diseño y la optimización de ítems según las necesidades específicas de medición (Baker, 2001).

En definitiva, el diagnóstico de la CCT es una herramienta que debe adaptarse a los objetivos y características de cada prueba, dependiendo de si buscamos un test diagnóstico, de selección o de seguimiento de progreso, los requerimientos de discriminación, cobertura del rango de habilidad y precisión pueden variar.

No obstante, en términos generales, cuando diseñamos o evaluamos un test, es fundamental asegurarnos de que su CCT cumpla, al menos, con las siguientes condiciones deseables:

1. Alta discriminación en el rango de interés, para diferenciar con claridad entre niveles de habilidad cercanos.
   
   
2. Cobertura simétrica (o acampanada) del continuo de habilidad que deseamos medir, evitando sesgos hacia ítems demasiado fáciles o difíciles.
   
   
3. Maximización de la precisión en los niveles clave de evaluación, reduciendo el error de estimación donde más importa.
   
   

Al verificar y optimizar estos aspectos siempre en función de los propósitos concretos de la evaluación garantizamos que nuestro instrumento ofrezca resultados fiables, válidos y útiles para la toma de decisiones (Hambleton & Swaminathan, 2010).

Métodos de estimación de la CCT

Existen varios métodos estadísticos para estimar los parámetros que definen la forma de la CCT a partir de los datos de respuesta de los examinados. Algunos de los enfoques más utilizados incluyen:

Métodos de máxima verosimilitud: Los métodos de máxima verosimilitud son ampliamente utilizados para estimar los parámetros de la CCT (Embretson & Reise, 2000). Estos métodos buscan encontrar los valores de los parámetros que maximizan la probabilidad (verosimilitud) de observar los patrones de respuesta obtenidos en los datos.

Los algoritmos iterativos como el de Newton-Raphson o el de puntuaciones son comúnmente empleados para encontrar las estimaciones de máxima verosimilitud de los parámetros de la CCT (Baker & Kim, 2004). Estos métodos requieren cálculos complejos, pero son eficientes y producen estimaciones consistentes e insesgadas cuando se cumplen los supuestos del modelo.

Métodos bayesianos: Los métodos bayesianos ofrecen un enfoque alternativo para estimar la CCT, combinando la información de los datos con distribuciones previas (a priori) sobre los parámetros del modelo (Béguin & Glas, 2001). Estas distribuciones previas pueden basarse en conocimiento teórico o empírico previo sobre los valores plausibles de los parámetros.

Los métodos bayesianos utilizan algoritmos de Cadenas de Markov Monte Carlo (MCMC) o métodos de cuadratura numérica para aproximar las distribuciones posteriores de los parámetros de la CCT (Sheng, 2008). Estos enfoques pueden ser computacionalmente intensivos, pero permiten una mayor flexibilidad en la especificación de modelos complejos.

Simulaciones con cadenas de Markov Monte Carlo: Las simulaciones con cadenas de Markov Monte Carlo (MCMC) son una herramienta para estimar la CCT y otros aspectos de los modelos IRT (Kim & Bolt, 2007). Estas simulaciones generan muestras aleatorias de las distribuciones posteriores de los parámetros del modelo, utilizando algoritmos como el muestreo de Gibbs o el algoritmo Metropolis-Hastings.

Las simulaciones MCMC permiten una estimación precisa de la CCT y sus incertidumbres asociadas, incluso en modelos complejos con múltiples parámetros (Fox, 2010).

Aplicaciones generales de la CCT

La Curva Característica del Test (CCT) es una herramienta fundamental en la Teoría de Respuesta al Ítem (IRT) que ofrece una visión global y detallada del funcionamiento de una prueba en su conjunto (Hambleton et al., 1991). Comprender y utilizar la CCT resulta esencial para desarrolladores de tests, psicómetras e investigadores, ya que permite evaluar el rendimiento de un instrumento a lo largo de todo el espectro de habilidades de los evaluados (Baker, 2001). Además, esta herramienta optimiza la medición al identificar los niveles de habilidad en los que la prueba muestra mayor capacidad de discriminacion, hecho crucial para adaptar los instrumentos a necesidades específicas de evaluación (De Ayala, 2009).

La CCT también facilita la comparación directa entre distintos tests o versiones de una misma prueba, proporcionando un criterio objetivo para la selección, validación y mejora continua de los instrumentos (Embretson & Reise, 2000). A partir de ella, es posible transformar las puntuaciones brutas en estimaciones precisas de la habilidad, lo cual mejora la interpretabilidad de los resultados (Lord, 1980). Asimismo, en el diseño de tests adaptativos computarizados, la selección de ítems se basa en la información que aporta la CCT, permitiendo que cada evaluado reciba una experiencia personalizada y eficaz (Wainer, 2000).

En conjunto, el análisis y uso adecuado de la CCT es indispensable para asegurar la calidad y utilidad de los instrumentos de medición en campos tan diversos como la educación, la psicología clínica y la selección de personal (Reckase, 2009). Además, su integración en el desarrollo de pruebas contemporáneas impulsa la innovación y la personalización de los procesos evaluativos, permitiendo a los especialistas identificar áreas de mejora y adaptar continuamente los instrumentos a las características específicas de cada población evaluada. Esta capacidad de ajuste y mejora continua convierte a la CCT en un aliado estratégico en el avance y refinamiento de las prácticas psicométricas.

Herramientas y software:

• R (paquete ltm): Permite ajustar modelos IRT unidimensionales (1PL, 2PL, 3PL) mediante máxima verosimilitud marginal. Incluye funciones como ltm(), factor.scores() y plot(), facilitando el cálculo y trazado de Curvas Características del Ítem (CCI) y del Test (CCT), además del diagnóstico de ajuste del modelo.
• jMetrik: Aplicación Java gratuita con interfaz gráfica que admite análisis clásico y moderno. Ofrece módulos para estimación de parámetros IRT, generación de ICCs y CCTs, reportes de fidelidad, información del test y análisis de sesgo diferencial. Ideal para quienes no tienen experiencia en programación.
• IRTPRO: Software comercial avanzado que utiliza algoritmos de máxima verosimilitud marginal (MML) y Bayesianos para modelos IRT multidimensionales. Proporciona un entorno gráfico para visualizar CCI, CCT y Funciones de Información del Test, además de herramientas de simulación y validación cruzada de parámetros.

Bibliografía

Abad García, F. J., Olea Díaz, J., Ponsoda Gil, V. y García García, C. (2011). Medición en ciencias sociales y de la salud. Madrid: Síntesis. doi: 9788497567275

Baker, F. B. (2001). The Basics of Item Response Theory. ERIC. https://edres.org/irt/baker/final.pdf

Baker, F. B., & Kim, S. H. (2004). Item response theory: Parameter estimation techniques. CRC Press. https://doi.org/10.1201/9781482276725

Béguin, A. A., & Glas, C. A. (2001). MCMC estimation and some model-fit analysis of multidimensional IRT models. Psychometrika, 66(4), 541-562. https://doi.org/10.1007/BF02296195

De Ayala, R. J. (2009). The Theory and Practice of Item Response Theory. Guilford Publications. https://archive.org/details/theorypracticeof0000deay

Embretson, S. E., & Reise, S. P. (2000). Item response theory for psychologists. Lawrence Erlbaum Associates Publishers. https://doi.org/10.4324/9781410605269

Fox, J. P. (2010). Bayesian item response modeling: Theory and applications. Springer Science & Business Media. https://doi.org/10.1007/978-1-4419-0742-4

Hambleton, R. K., & Swaminathan, H. (2010). Item Response Theory: Principles and Applications. Springer Science & Business Media. https://doi.org/10.1007/978-94-017-1988-9

Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of Item Response Theory. Sage. https://www.jstor.org/stable/1435166

Lord, F. M. (1980). Applications of Item Response Theory to Practical Testing Problems. Lawrence Erlbaum Associates. https://eric.ed.gov/?id=ED312280

Reckase, M. D. (2009). Multidimensional Item Response Theory. Springer. https://doi.org/10.1007/978-0-387-89976-3

Kim, J.-S., & Bolt, D. M. (2007). Estimating item response theory models using Markov chain Monte Carlo methods. Educational Measurement: Issues and Practice, 26(4), 38–51. https://doi.org/10.1111/j.1745-3992.2007.00107.x

Sheng, Y. (2010). Bayesian Estimation of MIRT Models with General and Specific Latent Traits in MATLAB. Journal of Statistical Software, 34(3). http://www.jstatsoft.org/v34/i03/paper

Wainer, H. (2000). Computerized Adaptive Testing: A Primer. Lawrence Erlbaum Associates. https://doi.org/10.4324/9781410605931