¿Cómo y cuándo hacer una prueba T para muestras independientes?

.

Por: Uriel Alejandro Arevalo Rochel

La prueba T es un estadístico que permite medir si hay diferencias significativas entre las medias de uno o dos grupos. Las muestras independientes, por su parte, son aquellas en las que las observaciones de un grupo no afectan ni están relacionadas con las observaciones del otro grupo. Por ejemplo, piense en el caso de dos grupos de personas, uno que ha tomado café y otro que no, usaremos una prueba T para muestras independiente en el caso de que queramos saber si hay diferencias significativas entre ambos grupos, evaluando si un grupo siente más o menos sueño después de un determinado periodo de tiempo.

Existen distintas formas de hacer una prueba T pero para todas ellas debemos cumplir algunas condiciones o supuestos. La primera de ellas es la normalidad, es decir, que los valores de nuestras muestras deben distribuirse de forma normal. La segunda es que el tamaño (n) de la muestra sea mayor a 30, es decir, que las muestras superen los 30 “participantes”. Finalmente, la tercera de ellas es que las varianzas de los grupos no tengan diferencias significativas, veamos un ejemplo.

Como hacer una prueba T con muestras independientes

La fórmula para el estadístico T con muestras independientes con n iguales o con diferencias en ellos, está dada por

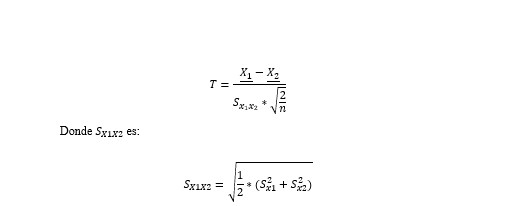
Estas fórmulas son un tanto engorrosas de utilizar por lo que, si usted cuenta con un programa estadístico, es muy probable que pueda hacer una T de una forma mucho más fácil.

Ejemplo de prueba T en JASP

En nuestro ejemplo, tenemos un grupo al que se le da a beber café y otro al que no se le da nada de tomar. Esto, para saber si el grupo al que se le administró el café tiene diferencias significativas con la segunda muestra al comparar su nivel de sueño (en nuestro ejemplo contamos con un n de 31 en nuestros dos grupos por lo que una de las condiciones ya se cumple). Las siguientes imágenes ilustran cómo realizar una prueba T en JASP, primero debemos tener los datos con los valores previamente cargados en JASP como en la siguiente imagen

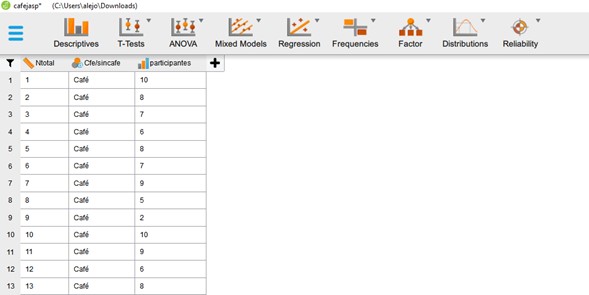
Una vez tengamos los datos cargados en JASP, como la imagen de arriba, debemos hacer clic en la opción “T-Tests” como en la siguiente imagen.

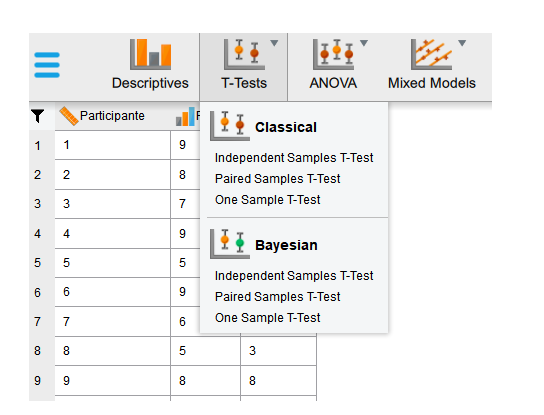
Después de tener cargados nuestros datos, debemos clickear en T-Tests y después en Independent Sample T-Tests como se muestra en la siguiente imagen:

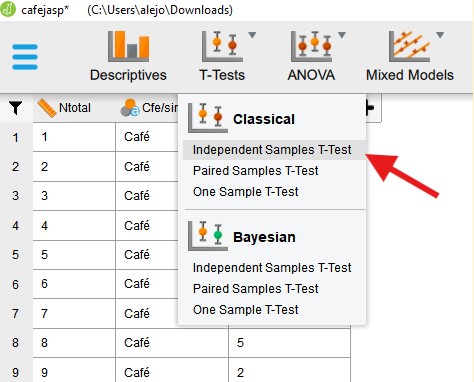
El siguiente paso para realizar la prueba T es pasar las variables y los tipos de grupos a sus respectivos lugares como podemos ver en la siguiente imagen:

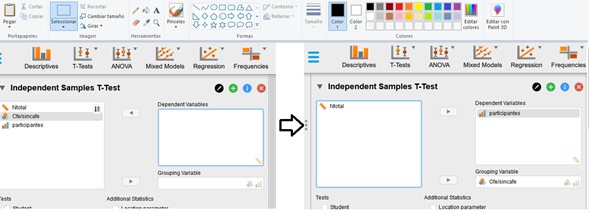
Después debemos asegurarnos de que nuestros datos cumplan con el supuesto de normalidad, para ello vamos a clickear en el botón “Normality”

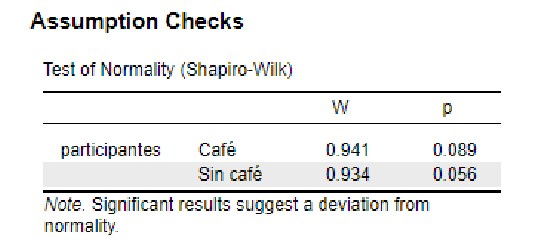
En la siguiente tabla se muestra la prueba de normalidad donde vemos que los dos valores p son mayores a 0.05 lo que nos hace aceptar nuestra hipótesis nula de normalidad

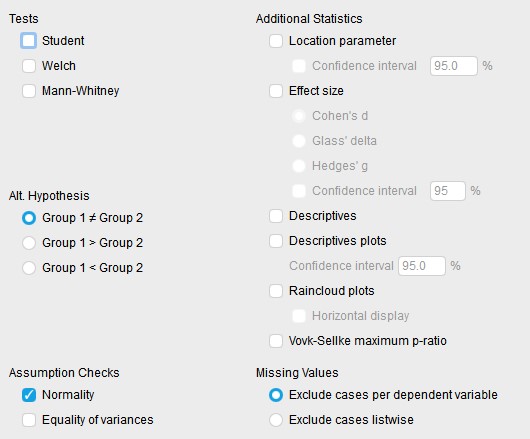
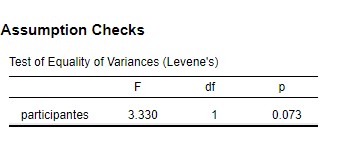
Después de este paso, debemos probar si tenemos diferencias significativas en nuestras varianzas, para ello damos click en el botón Equality of variances.

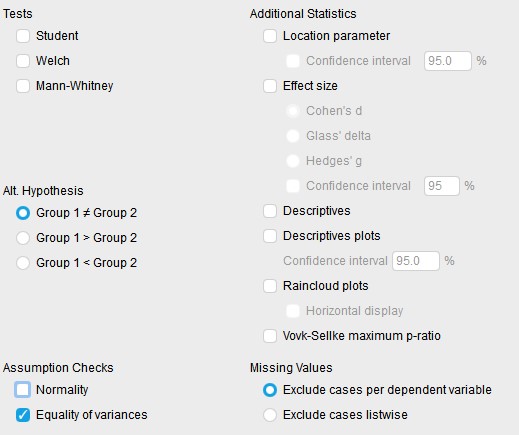
Y nos aseguramos de que nuestro valor p sea mayor a 0.05, en este caso nuestro valor p es de 0.073 lo que nos hace aceptar que no hay diferencia entre las varianzas de los grupos.

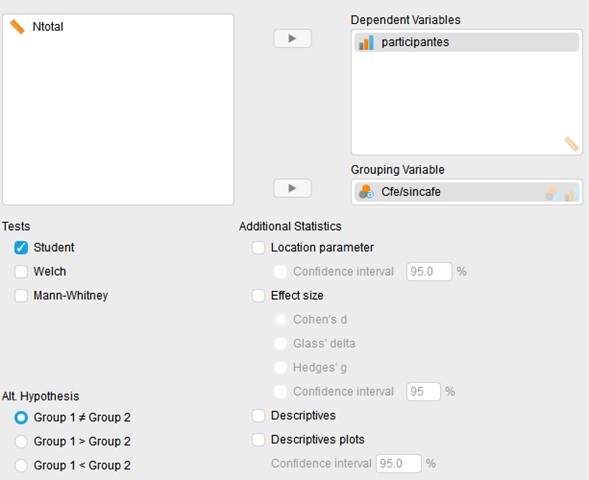
Habiendo comprobado que nuestros datos cumplen con los requisitos de una prueba T podemos realizarla dando click en el botón Student y asegurándonos que nuestra hipótesis alterna es que hay diferencias entre grupos clicamos la opción Grupo 1 ≠ Grupo 2

A continuación, solo debemos mirar nuestra tabla “Independent Samples T-Test”, como se muestra en la siguiente imagen. En ella es posible observar que el valor T es igual a 4.89,  los grados de libertad son 60 y el p valor es menor a 0.05, con lo cual tenemos evidencia suficiente para rechazar la hipótesis nula y aceptar la alterna, según la cuál existen diferencias significativas entre el grupo que bebió café y el que no en sus factores de sueño.

Bibliografía

DATAtab Team (2024). Prueba t para muestras independientes. https://datatab.es/tutorial/unpaired-t-test

Jmp Statistical Discovery (2024). La prueba t de dos muestras. https://www.jmp.com/es_co/statistics-knowledge-portal/t-test/two-sample-t-test.html

IBM (2023). Prueba T para muestras independientes. https://www.ibm.com/docs/es/spss-statistics/saas?topic=tests-independent-samples-t-test

UGR (2016). TÉCNICAS ESTADÍSTICAS APLICADAS EN NUTRICIÓN Y SALUD. https://www.ugr.es/~fmocan/MATERIALES%20DOCTORADO/testt2016.pdf