¿Por qué el valor p no lo es todo?

Por Brayam Pineda
Psicólogo. Especialista en Analítica de Datos.
Universidad Nacional de Colombia.

Hace algunos años la revista Basic and Applied Social Psychology (BASP) sorprendió con un anuncio, ya no iban a aceptar más estudios que reportaran el valor p. ¿Por qué? Bueno, pues porque consideraron que p < 0,05 es una barra muy fácil de alcanzar, y a veces, una excusa para que se produzcan investigaciones de menor calidad (Trafimow, D. y Marks, M., 2015). Aunque la controversia alrededor del hecho no se hizo esperar, este no es un hecho aislado. Desde antes de la muerte de Fisher ya había una fuerte discusión alrededor de este asunto, y este no es ni mucho menos el primer intento de escepticismo al respecto de estas mediciones en el campo de la psicología.

Un caso muy conocido es el de Lykken quien en 1968 ya había puesto en tela de juicio la ceguera alrededor de este requerimiento en las revistas académicas, partiendo de una crítica a un artículo publicado por Sapolsky en 1964 “quien proponía la “teoría cloacal del nacimiento”. En síntesis, Sapolsky proponía que los pacientes que presentan problemas de alimentación, como anorexia y bulimia, tenían una tendencia a la impregnación oral, lo cual dependía de su deseo inconsciente a embarazarse o no. La premisa era que los pacientes con desórdenes alimenticios mantenían una creencia inconsciente que hacía que vieran animales con cloacas en el test de Rorschach. Para probar su teoría, Sapolsky administró la prueba en mención a un grupo de pacientes en un hospital psiquiátrico “19 de los 31 que visualizaron una rana en el test tenían, de hecho, algún desorden alimenticio comparados con los 5 del grupo control. El análisis estadístico de los grupos reportó un chi cuadrado significativo”. Sobra decir que, pese a que los resultados fueron estadísticamente significativos, la relevancia clínica y el sustento teórico es débil, asunto que fue determinado por 20 colegas, quienes afirmaron que de hecho es improbable la teoría propuesta por Sapolsky (Sanchez-Escobedo, Pedro & Alvaro, & Ferrer, 1999).

Pese a las numerosas críticas recibidas, los valores p siguen siendo exigidos en la mayoría de las revistas científicas. No obstante, un buen número de estas piden acompañar este indicador de otros que hablen un poco más acerca de los datos y el alcance de las conclusiones. Le invito a ver algunas alternativas.

1. Intervalos de confianza

Los intervalos de confianza ofrecen mucha más información que las clásicas pruebas de hipótesis, por ejemplo, permiten conocer la magnitud y precisión del efecto observado. Así también, permiten hacer pruebas de hipótesis comparando la media y los intervalos del grupo control y experimental. Considere el ejemplo que señalan Gil y Castañeda (2005), en el cual un investigador está interesado en saber si la prevalencia de depresión es mayor en mujeres que en hombres. Basado en algunos estudios, encuentra que el  29,2% de las mujeres sufre depresión frente a un 19,6% de los hombres con un p < 0,001. Sin embargo ¿Cuánto más prevalente es en un grupo que en otro? ¿Es dicha diferencia clínicamente relevante? Estas preguntas no tienen respuesta usando la clásica prueba de hipótesis, ya que el valor p sólo determina si existen diferencias o no, y no informa sobre la magnitud de las mismas. Recuerde que un valor p menor no quiere decir que esos resultados sean más significativos que otros con un p valor mayor, sino que ambos se interpretan en virtud del nivel de significancia, siendo las posibles respuestas si hay diferencias significativas o no las hay.

Continuando con Gil y Castañeda (2005), es posible que un lector se vea tentado a restar una proporción de la otra y concluir que la diferencia es 9,6% mayor en mujeres respecto a los hombres “Sin embargo, este procedimiento es incorrecto debido a que las prevalencias… son valores encontrados en la muestra” por lo que al cambiar la muestra cambiarán las proporciones. Aquí es donde son útiles los intervalos de confianza, ya que permiten establecer un rango de valores en los cuales, con un nivel de confianza generalmente del 95%, se encontrará el parámetro de interés en la población en general. Para este ejemplo, el IC con un 95% de confianza se encuentra entre 7,4% y 11,8%, es decir que la prevalencia de depresión es mayor en mujeres que en hombres entre un 7,4 y un 11,8 por ciento. Como es posible observar, el investigador podría no usar pruebas de hipótesis sino únicamente IC en su estudio e igual llegaría a los mismos resultados con la posibilidad de brindar más información.

Pese a sus virtudes, los IC han recibido igual o tantas críticas como los valores p pues como señaló la BASP en cuanto a estos “el problema es que, por ejemplo, un intervalo de confianza del 95% no indica que el parámetro de interés tenga una probabilidad del 95% de estar dentro del intervalo. Más bien, significa simplemente que, si se tomara un número infinito de muestras y se calcularan los intervalos de confianza, el 95% de los intervalos de confianza capturarían el parámetro de la población. De manera análoga a cómo el test de prueba de hipótesis no proporciona la probabilidad de la hipótesis nula, que es necesaria para proporcionar un caso sólido para rechazarla” (Trafimow, D. y Marks, M., 2015, p. 1).

2. Tamaño del efecto

Como ya hemos visto, los intervalos de confianza nos permiten obtener mayor información respecto a los valores p. Imagine ahora que usted decide probar una nueva pedagogía en un aula de clase, hace las comparaciones necesarias y concluye que es posible que la media del grupo experimental se encuentre en un rango entre 10 y 15 puntos arriba del grupo control, sin embargo ¿Qué tanto son 10 o 15 puntos? Bien, pues eso depende de la escala de medida. Si por ejemplo la escala de medida va de 1 a 100, posiblemente aumentar 10 puntos sea un avance deseable, pero si va de 0 a 500 no lo sea tanto. En este sentido, el problema con los IC es que están expresados en términos de las unidades originales, alguien que desconozca los detalles del estudio tendrá dificultades para valorar su significancia práctica.

El tamaño o magnitud del efecto es una forma de cuantificar la efectividad de una intervención particular. Es decir, es un estadístico que nos dice qué tanto afecta el cambio en la variable independiente a la dependiente basado en la distribución de los datos. En palabras de Coe (2003) “La magnitud del efecto cuantifica el tamaño de la diferencia entre dos grupos, y por lo tanto se puede decir que es una verdadera medida de la significancia de tal diferencia” (p. 159).

Existen múltiples indicadores de la magnitud del efecto, todos ellos pueden agruparse en cuatro tipos: 1. Índices de diferencias entre grupos, 2. Índices de fuerza de asociación, 3. Índices ajustados y 4. Estimaciones de riesgo.  Dominguez-Lara (2021) ofrece una guía espectacular para guiarse a la hora de escoger el indicador que esté más acorde al tipo de investigación, así como los valores usualmente aceptados por cada índice para considerar si el efecto es pequeño, mediano o grande. No obstante, la significancia práctica real de cada investigación está dada por el contexto en el que surge y no por los valores del efecto como tal.

Reportar la magnitud del efecto en las investigaciones debería ser más que una opción, una obligación ya que es posible realizar metaanálisis de las investigaciones que han sido replicadas con el fin de obtener una mejor estimación global del efecto. Cabe anotar también, que estos índices suelen ser muy susceptibles a los supuestos de normalidad por lo que es necesario que siempre se dejen claros estos aspectos, así como el margen de error probable o intervalo de confianza.

3. Potencia estadística

Quizá usted haya escuchado hablar alguna vez o entienda más o menos qué son los intervalos de confianza, y seguramente el tamaño del efecto lo ha leído en varios papers, pero ¿y qué me dice de la potencia estadística? Es una pregunta capciosa por supuesto, ya que este es quizá el concepto y cálculo estadístico que menos se reporta en las investigaciones que se publican a diario.

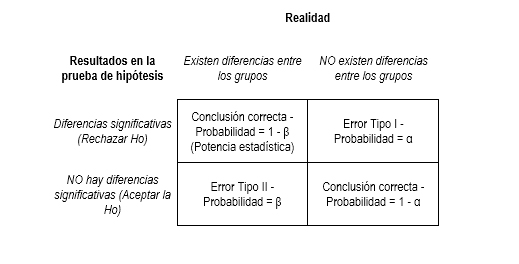
La potencia estadística es una cuantificación en términos de probabilidades de que un diseño investigativo detecte diferencias estadísticamente significativas o efectos allí donde los haya (Quezada, 2007). Para hacerlo más sencillo, veamos la siguiente tabla (que de seguro le resulte familiar)

En términos prácticos la potencia se expresaría como

Potencia = P(Rechazar Ho | Ho es falsa)

probabilidad de rechazar la hipótesis nula dado que es falsa.

Otra forma de verla es

Potencia = 1 – P(no rechazar Ho | Ho es falsa)

Uno menos la probabilidad de no rechazar la hipótesis nula dado que es falsa. O, la probabilidad de No cometer un error tipo II.

Ahora bien, así como existen valores convencionales de un α (0,05), existe también un valor convencional de β, el cual es de 0,20. Entendiendo la potencia como 1- β, el nivel convencional deseado de la potencia es 0,8. Pero ¿y cómo se calcula la potencia? Se calcula con base en el tamaño de la muestra n, la magnitud del efecto deseado y el Alpha.

Existen dos momentos en los que usted puede calcular la potencia de su estudio, antes o después de realizarlo. Si usted lo calcula antes, este indicador le permitirá conocer el tamaño de la muestra mínimo necesario para evitar cometer error Tipo II, de esta manera, si usted ya cuenta con el n establecido, la potencia le permitirá saber si vale la pena o no, continuar con su investigación antes de empezar. Por otro lado, si usted lo calcula posteriormente, sirve para determinar la probabilidad que tuvo su estudio de haber cometido error Tipo II, esto es especialmente útil cuando sus resultados no fueron estadísticamente significativos.

Existen software de licencia gratuita especializados en el cálculo de este indicador, y aunque parece una buena noticia, de fondo esconde una mala. La mala es que la mayoría de software de análisis de datos no contienen este índice entre sus cálculos, y es necesario recurrir a software externos. Lo anterior, aunado al poco énfasis que los docentes universitarios hacen al respecto del mismo, ha hecho que sea un indicador olvidado, aunque cada vez más las revistas científicas lo estén requiriendo.

En resumen, pese a que los p valores son sin duda alguna una herramienta estadística de mucho valor, no son suficientes para reportar adecuadamente los resultados de una investigación, por lo que siempre es buena idea reportar indicadores adicionales que den una mejor idea de lo hallado. Ahora bien, reportar esta información no sólo agrega solidez a la evidencia aportada, sino que permite realizar metaanálisis y contribuye a la transparencia de la ciencia, es por ello que le invitamos a siempre acompañar sus investigaciones de estos tres indicadores.

Bibliografía

Alonso Trujillo, J., Cuevas Guajardo, L., & Alonso, A. (2017). Uso del ritual de la significancia estadística y su impacto sobre el aprendizaje de la misma. Revista CuidArte, 6(12), 16.

Clark, M. L. (2004). Los valores P y los intervalos de confianza:¿ en qué confiar?.

Coe, R., & Soto, C. M. (2003). Magnitud del efecto: Una guía para investigadores y usuarios. Revista de Psicología, 21(1), 145-177.

Dominguez-Lara, S., 2021. Magnitud del efecto, una guía rápida. [online] Available at: <http://10.1016/j.edumed.2017.07.002> [Accessed 18 October 2021].

Gil, J. F., & Castañeda, J. A. (2005). Una mirada al valor de p en investigación. Revista Colombiana de Psiquiatría, 34(3), 414-424

Quezada, Camilo (2007). POTENCIA ESTADÍSTICA, SENSIBILIDAD Y TAMAÑO DE EFECTO: ¿UN NUEVO CANON PARA LA INVESTIGACIÓN?. Onomázein,  (16),159-170.[fecha de Consulta 17 de Octubre de 2021]. ISSN: 0717-1285. Disponible en:   https://www.redalyc.org/articulo.oa?id=134516684004

Sanchez-Escobedo, Pedro & Alvaro, & Ferrer, J. (1999). SIGNIFICANCIA ESTADÍSTICA EN LA INVESTIGACIÓN PSICOEDUCATIVA.

Trafimow, D. y Marks, M. Basic Appl. Soc. Psicoanalizar. 37 , 1-2 (2015).