Regresión lineal múltiple.

¿Cómo y cuándo hacer una regresión múltiple? – Ejemplo en JASP

.

Por: Aylen Zarhek Gutiérrez Nova

En la vida, rara vez una sola variable explica por completo el cambio observado en otra. Por lo general, es la interacción entre múltiples factores la que determina el desarrollo de un fenómeno.

En este sentido, en ciertas investigaciones, estudios o experimentos no es posible utilizar el modelo de regresión lineal simple debido a que suele necesitar estudiar varias variables para explicar la variable de interés. Cuando éstas varían siguiendo algún patrón, la regresión múltiple es útil para establecer el efecto de una variable independiente, en tanto que sus similares se mantienen constantes (Pérez-Tejada, 2008).

Al incorporar más de una variable independiente en nuestros análisis, logramos explicar mejor los cambios en la variable dependiente y, como resultado, podemos realizar predicciones más precisas.

¿Qué es la regresión múltiple?

La regresión lineal múltiple se puede considerar como una generalización, o extensión, de la regresión lineal simple a situaciones donde hay una variable dependiente y más de una variable independiente.

Es decir, en lugar de usar sólo una variable independiente x, se emplean simultáneamente varios factores de predicción, y se busca cuál es la combinación entre estos que predice mejor una variable dependiente y. Así, se puede ser capaz de explicar más de la varianza de la variable dependiente, y tener con ello un modelo que permitiría una predicción más precisa (Clark-Carter, 2002; Mendenhall, 2010).

¿Para qué son útiles los análisis de regresión lineal múltiple?

• Estos modelos permiten explicar y predecir el valor de una variable a partir de las puntuaciones de múltiples factores que podrían influir en esta; así como describir el grado relativo en que una serie de variables contribuyen a explicar un fenómeno y estimar cuál es la independiente que mejor predice las puntuaciones de la dependiente (Betanzos y López, 2017; Clark-Carter, 2002; Hernández-Sampieri, 2018; Mendenhall, 2010).
• Es posible que exista una superposición entre las x en la varianza explicada para la y. En consecuencia, algunas variables independientes pueden no aportar mucho al modelo de regresión, sugiriendo que la varianza es explicada por otras variables (Clark-Carter, 2002).

Suposiciones del modelo.

• Linealidad. Cada predictor tiene que estar linealmente relacionado con la variable dependientemientras los demás predictores se mantienen constantes, de lo contrario no se puede introducir en el modelo. La forma más recomendable de comprobarlo es realizando los diagramas de dispersión parcial de cada variable independiente (Amat-Rodrigo, 2016; Vilà et al., 2019).
• Independencia de los errores. Los errores en la medición de las variables predictoras son independientes entre sí. Se verifica mediante el test de hipótesis de Durbin-Watson (Amat-Rodrigo, 2016; Vilà et al., 2019).
• Homocedasticidad. La varianza de los errores debe permanecer constante. Para comprobarlo, se presenta un gráfico de dispersión, y se comprueba que los residuos se distribuyen aleatoriamente, manteniendo una misma dispersión y sin patrones específicos (Amat-Rodrigo, 2016; Vilà et al., 2019).
• Normalidad. Implica que hay una distribución normal de los residuos, con una media de cero. Para comprobarlo se hace uso de la prueba Kolmogorov-Smirnov, o se recurre a histogramas y a los cuantiles normales (Amat-Rodrigo, 2016; Vilà et al., 2019).
• No colinealidad. Los predictores deben ser independientes de los otros, de lo contrario, los valores predichos por el modelo resultan más inestables. Ocurre multicolinealidad entre las variables cuando existe una fuerte correlación entre las mismas; no solamente en correlaciones dos a dos, sino a cualquiera de ellas con cualquier grupo de las restantes (Clark-Carter, 2002; Vilà et al., 2019). Los estadísticos de colinealidad, tolerancia y el factor de inflación de la varianza (VIF, por sus siglas en inglés) comprueban este supuesto.

Debido a que el análisis de regresión lineal múltiple, habitualmente se genera con ayuda de un programa por computadora, se suele generar primero el modelo y posteriormente validar las suposiciones del mismo. Para este propósito, deben verificarse las gráficas residuales generadas para asegurarse que sean válidas todas las suposiciones de la regresión lineal (Mendenhall, 2010).

Adicionalmente, se debe tener en cuenta otras condiciones que podrían influenciar la capacidad de predicción del modelo de regresión múltiple:

• Tamaño de la muestra. Si no se dispone de las suficientes observaciones, predictores que no son realmente influyentes podrían parecerlo. En general, cuantas más observaciones, más predictores se pueden incorporar (Clark-Carter, 2002).
• Valores atípicos con una fuerte influencia. Es importante identificar aquellas observaciones que sean atípicas y puedan influir en los resultados. La forma más fácil de detectarlos es a través de las gráficas de residuos (Amat-Rodrigo, 2016).
• Escala de las variables. Las variables predictoras deben ser cuantitativas, de intervalo o razón; mientras que la variable de interés, debe ser cuantitativa de intervalo. (Mendenhall, 2010; Parra-Pulido, 2019)

Método de análisis.

Existen diferentes maneras de realizar una regresión múltiple, dependiendo de cómo se elige incorporar las variables independientes al modelo. Debido a que el modelo final puede depender del método utilizado, la decisión más adecuada es elegir el método que mejor se ajuste a las expectativas teóricas y empíricas que subyacen a la investigación (Betanzos, 2017).

Si las variables predictivas no están correlacionadas, no importa el orden en que se introduzcan. Sin embargo, en la mayoría de los casos, estas variables se encuentran correlacionadas en alguna medida y, por ello, el orden en el que se introduzcan al modelo puede tener consecuencias (Clark-Carter, 2002; Goss-Sampson, 2019; Parra-Pulido, 2019).

1. Regresión Estándar, o entrada forzada. (“Enter”)

En este método, simplemente se incorporan todas las variables independientes en el modelo en el orden en que se encuentran en la computadora. Resulta muy útil cuando se pretende explicar en lo posible la varianza de la VD y no se desean tomar medidas que agreguen información (Clark-Carter, 2002; Goss-Sampson, 2019).

2. Regresión Jerárquica, o entrada por bloques. (“Hierarchical entry”)

Previo a la incorporación de las variables predictoras, el investigador deberá contar con un orden preestablecido, determinado mediante un trabajo y conocimientos previos que tenga el investigador sobre el constructo teórico en que se basa. Así, se decide el orden en que se introducen las variables independientes en función de su importancia en la predicción de la variable resultado. En pasos posteriores, es posible introducir variables predictoras adicionales (Clark-Carter, 2002; Goss-Sampson, 2019; Parra-Pulido, 2019).

El resultado de este modelo, puede generalizarse y aplicarse en la construcción de otro. Así, una variable dependiente en una regresión puede volverse una variable independiente. De esta manera, puede efectuarse un análisis de trayectoria según los datos (Clark-Carter, 2002).

3. Regresión estadística múltiple.

Las decisiones sobre el orden en que se introducen las variables predictoras al modelo se basan en cierto criterio estadístico. Estos métodos pretenden dar como resultado la combinación de variables independientes que expliquen la cantidad máxima de varianza de la variable dependiente, omitiendo de la ecuación aquellas variables independientes que no contribuyan de manera significativa al modelo. Los métodos de regresión estadística múltiple se usan únicamente cuando el investigador explora la información y no busca probar un modelo específico (Clark-Carter, 2002; Parra-Pulido, 2019).

Encontramos tres tipos de incorporación de las variables:

• Método de avance o hacia adelante. (“Forward”)

Este método incorpora las variables predictoras una a la vez en el modelo, con base en la importancia relativa que tiene cada variable dentro del modelo de regresión lineal múltiple. Es decir, se escogen las variables que explican la mayor parte de la varianza de la variable dependiente (Clark-Carter, 2002; Goss-Sampson, 2019).

En primer lugar, se introduce la variable predictora que tiene la correlación simple más alta con la variable dependiente. Si este predictor mejora significativamente la capacidad del modelo para predecir el resultado, entonces el predictor se retiene en el modelo y se busca el siguiente predictor.

Una vez que la primera variable se incorporó, la siguiente que se selecciona es aquella con la mayor correlación semiparcial respecto a la variable dependiente. Es decir, se escoge el predictor que explique la mayor parte de la varianza restante, pues al modelo no le importa el porcentaje que ya está explicado. El predictor que representa la variación más grande se agrega al modelo si hace una contribución significativa (Betanzos y López, 2017; Clark-Carter, 2002; Goss-Sampson, 2019; Parra-Pulido, 2019).

Este proceso continúa hasta que ninguna de las demás variables contribuya significativamente al modelo.

• Método de eliminación o hacia atrás. (“Backward”)

Es opuesto al método de avance. En este método, primero se ingresan todas las variables predictoras en el modelo y, de manera secuencial, se evalúa la pertinencia de eliminar del modelo de regresión múltiple cada una de las variables.

Inicialmente, tras ingresar todas las variables se calcula la contribución que hace cada una de ellas al modelo. Si una de ellas no está haciendo una contribución estadísticamente significativa, se elimina y se evalúa si hay una reducción significativa de la varianza explicada. Si dicho retiro no demerita en forma significativa el modelo, se elimina tal variable. Posteriormente, se repite el proceso hasta que se eliminen las variables predictoras que cumplen con el criterio de eliminación previamente descrito (Betanzos y López, 2017; Clark-Carter, 2002; Goss-Sampson, 2019; Parra-Pulido, 2019).

De este modo, en el modelo sólo se conservan las variables predictoras que tienen una importancia estadísticamente significativa en la explicación de la variable dependiente.

Este modelo puede ser útil para explorar variables predictoras no utilizadas previamente o para afinar el modelo con el fin de seleccionar las mejores de entre las disponibles (Goss-Sampson, 2017).

• Método secuencial o paso a paso. (“Stepwise”)

Se puede considerar como la versión mejorada de los dos métodos anteriores, y el método más seguro de los tres, puesto que revalora la contribución de las variables previamente incorporadas, cada vez que se agrega una al modelo. Esto es particularmente relevante, ya que es posible que una variable que se integró al modelo al principio de la evaluación, en etapas posteriores no realice una contribución significativa al modelo, debido a su relación con las variables que se integraron posteriormente (Betanzos y López, 2017).

Este método es útil cuando no se prueba un modelo explícito, sino cuando se exploran los datos para encontrar el modelo que explique la mayor cantidad de varianza de la variable de interés, usando el menor número de variables independientes (Clark-Carter, 2002).

Guarda una gran similitud con el método de avance, en tanto ambos incorporan las variables una a la vez al modelo. Sin embargo, en el método paso a paso, cada vez que se agrega cada variable predictora, se realiza una evaluación de todas las ya incorporadas, y se elimina la variable recién añadida antes de que no contribuya significativamente. De este modo, el modelo se reevalúa constantemente para comprobar si se pueden eliminar los predictores redundantes (Betanzos, 2017; Clark-Carter, 2002; Goss-Sampson, 2019; Parra-Pulido, 2019)

Medidas de la bondad de ajuste.

La bondad de ajuste es el porcentaje de variabilidad explicado por el modelo. Antes de examinar las medidas estadísticas de bondad de ajuste, es recomendable revisar las gráficas de residuos. Cuando estas pasan la revisión de supuestos, se puede confiar en los resultados numéricos y verificar la bondad de ajuste estadística (Betanzos y López, 2017).

En la regresión múltiple, comúnmente se emplean como medidas el coeficiente de determinación y el estadístico F.

• El coeficiente de determinación (R²) representa la proporción de variabilidad de la variable dependiente explicada por el modelo de regresión, o el grado en que los datos observados se ajustan al modelo (Amat-Rodrigo, 2016).

Toma valores entre 0 y 1. Si todas las observaciones se encuentran sobre el modelo construido, R² es igual a 1. Esto es, cuanto más se acerca a uno, más poder explicativo tiene el modelo. Sin embargo, si R² tiene un valor cerca de cero o cero, nos indica que no existe una relación lineal sobre las variables, no necesariamente indica que no existe una relación entre ellas.

Cuando hay un elevado número de variables predictoras, el valor de R² aumenta. Por tal motivo, es una práctica común hacer una corrección al valor de R², conocida como R² corregida. Este coeficiente ajusta el número de observaciones y el número de variables independientes incluidas en el modelo de regresión, penalizando el número de variables predictoras incluidas (Betanzos y López, 2017; López, s.f.; Vilà et al., 2019).

• Desde el resumen del ANOVA, la prueba F evalúa la hipótesis de que el modelo no explica ninguna variación en la variable dependiente. Es decir, que no existe una relación lineal significativa entre la variable dependiente y el conjunto de variables predictoras que hacen parte del modelo, lo cual implicaría que la pendiente del plano de regresión es igual a cero (horizontal) (Betanzos y López, 2017).

De este modo, la prueba F permite valorar si la adición de uno o más predictores mejora significativamente el ajuste del modelo. Si el valor de F es grande, y el valor p es pequeño (> 0,05), podemos concluir que el modelo es significativo, y explica alguna variación de la variable dependiente, rechazando así la hipótesis nula (Betanzos y López, 2017; Vilà et al., 2019)

Interpretaciones erróneas.

Debido a la gran cantidad de información sobre Regresión Lineal Múltiple, es probable que nos encontremos con algunas contradicciones. A continuación, se presentan algunos errores de interpretación que debemos evitar al analizar nuestros datos:

• Cuando las variables incluidas en el modelo no son significativas, no necesariamente se debe a que aportan poca o ninguna información en la predicción de la variable dependiente. Las variables pueden ser importantes para el modelo, pero pueden haberse introducido en un orden erróneo.
• Es necesario tener cuidado de no concluir relaciones de causalidad entre las variables predictoras del modelo y la variable dependiente. Las relaciones causales pueden ser detectadas sólo con experimentos cuidadosamente diseñados. En casi todos los análisis de regresión, en los que no se diseñó un experimento, no hay garantía de que una variable predictora importante cause un cambio. Es posible que alguna variable que ni siquiera esté en el modelo sea la causante de esta relación.

Ejemplo

Un estudio quiere generar un modelo que permita predecir el promedio de las calificaciones de un estudiante, en función de diferentes variables. Se dispone de información sobre el promedio de las calificaciones del período escolar anterior, junto con resultados de otras pruebas tomadas a cada estudiante e información sobre su vida cotidiana. En concreto, de cada estudiante se conoce: el promedio de sus calificaciones, el número de horas que duermen a la semana, el número de horas que dedican a actividades de ocio, su puntaje de la escala de inteligencia WAIS, su puntaje en una prueba que determina dificultades de lectura y su puntaje en un test de autoestima.

1. Para comenzar, debemos abrir el archivo con nuestros datos, que previamente debió ser guardado en formato separado por comas.

(Menú Principal. Abrir. Ordenador. Buscar. Nombre del archivo. Abrir).

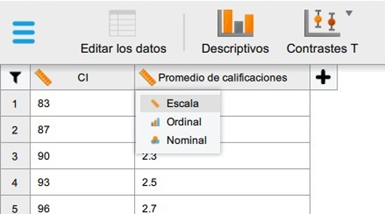
2. continuación, verificamos que la escala de las variables se encuentre correctamente, y realizamos cambios de ser necesarios.

3 Damos clic en la opción Regresión del menú superior. Luego, en el apartado clásico, damos clic en correlación.

El primer paso a la hora de crear un modelo lineal múltiple es analizar la relación que existe entre variables. Comenzaremos por comprobar si efectivamente existen relaciones significativas entre las variables predictoras y nuestra variable de interés. Esta información es crítica a la hora de identificar cuáles pueden ser los mejores predictores para el modelo, y para detectar colinealidad entre predictores. Además, es recomendable analizar la distribución de cada variable.

1. Ubicamos nuestras variables en la caja de asignación. Tras esto, hacemos una revisión del supuesto de normalidad y el valor de las correlaciones entre la variable dependiente y cada una de las variables independientes.

Añadiremos en primer lugar nuestra variable dependiente, y luego el resto de variables con que trabajaremos. Así, las primeras correlaciones que encontremos en JASP serán aquellas que tenemos que analizar.

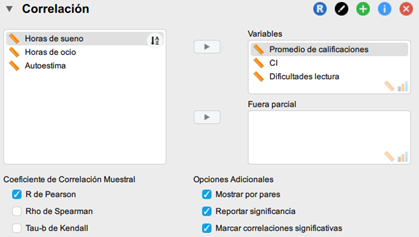
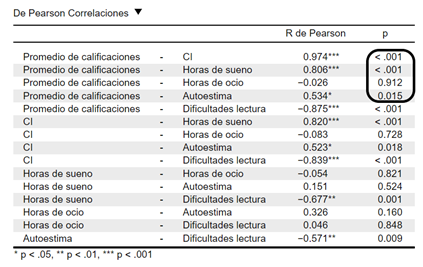
En este caso, encontramos que la correlación del CI, las Dificultades de lectura, las Horas de sueño y el Autoestima es significativa con el Promedio de calificaciones. Por otra parte, las Horas de ocio no se encuentran significativamente relacionadas al Promedio de calificaciones, puesto que su valor-p es mayor al valor crítico establecido (p < 0.05); y, por lo tanto, será una variable que no incluiremos en nuestro modelo de regresión. Para realizar el análisis de regresión lineal, volveremos a dar clic en la opción Regresión del menú superior. Luego, en el apartado clásico, damos clic en regresión lineal

Ubicamos nuevamente nuestras variables en la caja de asignación, sólo que en este caso haremos la distinción entre variable dependiente (promedio de las calificaciones), y las variables independientes (CI, Horas de sueño, Dificultades en lectura, Autoestima). La variable Horas de ocio no se incluye en el modelo porque su correlación con nuestra variable de interés, Promedio de calificaciones, no resultó significativa.

1. Elegimos el método con el que vamos a construir nuestro modelo. Debido a que el modelo final puede depender del método utilizado, la decisión más adecuada es elegir el método que mejor se ajuste a las expectativas teóricas y empíricas que subyacen a la investigación.
   

Para este ejemplo, usaremos el método Enter. Este es el método predeterminado de JASP, en el que todos las variables predictoras se introducen en el modelo en el orden en que aparecen en la caja Covariables.

2. Marcamos las siguientes opciones en los estadísticos, e inspeccionamos sus valores en las tablas que nos proporciona JASP.

Los resultados que obtenemos nos permiten analizar nuestro modelo de regresión lineal, y verificar que se estén cumpliendo los supuestos.

La primera tabla a considerar es la tabla de Coeficientes. En esta podemos observar si las variables predictoras incluidas en el modelo realizan un aporte significativo al modelo, es decir, cuando el estadístico No tipificado es significativamente diferente a cero. De este modo, que el valor p sea mayor a 0.05 nos indica que las variables no están contribuyendo significativamente al modelo, y por consiguiente no deberían hacer parte de este.

Por su parte, los estadísticos de colinealidad, tolerancia y FIV, comprueban el supuesto de multicolinealidad. Como regla general, si el FIV > 10 y la tolerancia < 0,1, el supuesto ha sido ampliamente violado. Si el promedio de los valores del FIV > 1 y la tolerancia < 0,2, el modelo podría estar sesgado.

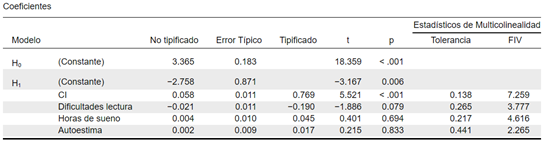
En nuestro análisis, vemos que solo el Coeficiente Intelectual muestra una contribución significativa al modelo inicial. Por ello, procedemos a eliminar las variables no significativas restantes. No obstante, dado que el p-valor de las variables puede cambiar al eliminar una, el proceso debe realizarse de forma gradual, eliminando una variable a la vez.

Retiramos la variable Autoestima, ya que presentaba el p-valor más alto. Tras este paso, observamos que: Horas de sueño seguía sin ser significativa, mientras que Dificultades de lectura, que antes no era significativa, ahora muestra un p-valor significativo. Al eliminar Horas de sueño, el p-valor de Dificultades de lectura disminuye aún más, reforzando su relevancia en el modelo.

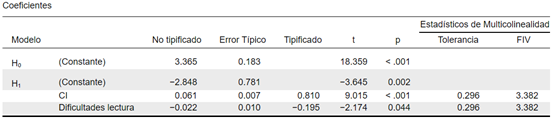
De este modo, el modelo final quedó compuesto por dos variables predictoras: Coeficiente Intelectual y Dificultades de lectura.

Sobre los estadísticos de colinealidad podemos concluir que, aunque la tolerancia es mayor a 0.2, el promedio del FIV es grande (3.382), lo que nos indica que debemos tener cuidado con que este modelo esté sesgado.

Continuando con nuestro análisis, nos encontramos con la tabla Resumen del Modelo. El valor de R² Ajustado indica el porcentaje de varianza explicado por el modelo. Así, encontramos que el modelo final, con dos variables, predice un 95,5% de la varianza del Promedio de las calificaciones. El estadístico Durbin-Watson comprueba que las correlaciones entre los residuos se encuentran entre 1 y 3, como se requiere. En nuestra tabla podemos observar que el valor de este estadístico es de 2.285, lo que sugiere una ligera tendencia negativa. No obstante, no hay autocorrelación significativa en los residuos (p = 0.771).

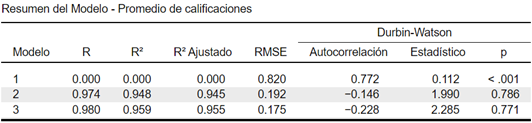
La tabla de ANOVA muestra que el estadístico F es significativo p < 0.001, sugiriendo que el modelo es adecuado que predice significativamente el Promedio de las calificaciones del estudiante.

Por último, si nuestra tabla de diagnóstico por casos está vacía, son buenas noticias. Esta tabla muestra los casos (filas) con residuos que se encuentren a 3 o más desviaciones estándar respecto a la media. Los casos con los errores más grandes podrían ser valores atípicos.

1. Finalmente, seleccionamos las gráficas de residuales, y verificamos que no se estén incumpliendo los supuestos de normalidad, y varianza constante.

Para que se cumpla el supuesto de normalidad, los puntos deben acercarse a la recta lo más posible en el “Gráfico Q-Q de los Errores Tipificados”. En el gráfico “Errores vs. Predicho” debemos revisar que la nube de puntos no siga algún patrón de cono o embudo, pues esto indica que no se está violando el supuesto de varianza constante, o homocedasticidad.

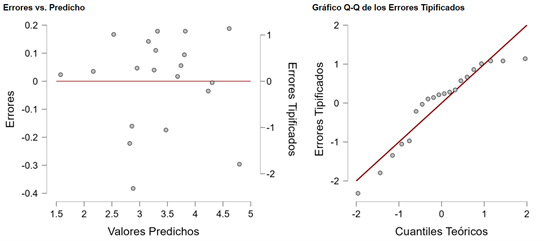
Concluyendo nuestro ejemplo, encontramos que a partir del Coeficiente Intelectual y el desempeño de los estudiantes en la prueba que determina dificultades en la lectura podemos predecir el promedio de las calificaciones de un estudiante.

Referencias

Amat-Rodrigo, J. (2016, julio). Introducción a la Regresión Lineal Múltiple. Ciencia de Datos. https://cienciadedatos.net/documentos/25_regresion_lineal_multiple#Variables_nominalescateg%C3%B3ricas_como_predictores

Betanzos, F. G., y López, J. K. C. (2017). Estadística aplicada en psicología y ciencias de la salud. Editorial El Manual Moderno.

Clark-Carter, D. (2002). Investigación cuantitativa en psicología: del diseño experimental al reporte de investigación. Oxford University Press.

Goss-Sampson, M. A., y Meneses, J. (2019). Análisis estadístico con JASP: Una guía para estudiantes.

Hernández-Sampieri, R. (2018). Metodología de la investigación: las rutas cuantitativa, cualitativa y mixta. McGraw Hill México

Mendenhall, W., Beaver, R. J., y Beaver, B. M. (2010). Introducción a la probabilidad y estadística. 13ª. Edición. México: Cengage Learning.