¿Cómo y cuándo hacer un ANOVA de muestras independientes?

.

Por: Uriel Alejandro Arevalo Rochel

En blogs pasados vimos en qué caso hacer o no hacer una prueba t, tanto con muestras independientes como con muestras dependientes, pero ahora surge una pregunta importante ¿qué debemos hacer cuando nuestros datos tienen tres o más grupos y nuestras medidas son independientes?

Un estudiante poco experimentado pero astuto podría responder esta pregunta de una forma muy fácil pero descuidada argumentando que puede hacer tantas pruebas t como sean necesarias para cada uno de los grupos y mirar si existe una diferencia significativa entre ellas, pero póngase a pensar un momento; imaginemos por un instante que el estudiante tiene razón y tratamos de hacer pruebas t para responder si existen diferencias entre los grupos, con tres grupos usted debería hacer tres pruebas t diferentes para responder a la incógnita, con 4 debería hacer 6 pruebas t y con un grupo de cinco debería hacer 10 pruebas t. Aunque contemos con programas estadísticos que pueden hacer pruebas t en segundos, a la larga el método de hacer pruebas t “infinitas” en inviable, tanto por la cantidad absurda de pruebas como por otro detalle importante: hacer este procedimiento de “infinitas” pruebas t aumenta el error tipo 1 (rechazar una hipótesis nula siendo esta verdadera) que podemos llegar a tener al reportar nuestros resultados.

Entonces si no podemos hacer pruebas t “infinitas” ¿cómo podemos proceder? La respuesta es hacer un análisis de varianza más conocido como ANOVA de muestras independientes, este análisis de varianza nos permite comparar más de dos grupos que dependen de un solo factor sin tener que preocuparnos por elevar la probabilidad de cometer un error tipo 1 en nuestra prueba. Ahora que sabemos en qué caso probablemente debemos utilizar una ANOVA, debemos tener presente los supuestos que deben cumplir nuestros datos para aplicarla.

El primero de ellos es la normalidad de nuestros datos ya que el ANOVA es una prueba paramétrica; el segundo de ellos es la independencia de nuestros datos, y el tercero es la homogeneidad de nuestra varianza en todos los grupos, en otras palabras, la homocedasticidad de los mismos, una vez cumplamos con estos tres supuestos, podemos empezar con nuestro análisis de varianza.

 Ahora, la forma de calcular dicho análisis de varianza se basa en encontrar una proporción entre la media cuadrática inter y la media cuadrática intra de nuestros datos, dicha proporción nos da como resultado en estadístico F de Fisher dada por la siguiente fórmula

Después de este cálculo solo debemos ir a una tabla de equivalencia donde, con ayuda de los grados de libertad, podremos tener nuestro p-valor, esto siempre y cuando queramos calcular nuestra ANOVA con lápiz y papel; otra opción que podemos utilizar para poder hacer un análisis de varianza es con ayuda de un programa estadístico y en este caso utilizaremos JASP.

Imagine usted que es un investigador y quiere saber si la habilidad de una persona en un video juego se ve afectada por el número de horas que juega en el día, la habilidad para este caso se mide con las puntuaciones que gana una persona en un día al jugar un minijuego, y para responderse la pregunta limita las horas de juego de las personas dividiendo a los participantes en tres grupos, los que juegan 3 horas al día, los que juegan 6 horas al día y los que juegan solo una hora al día, los datos son los siguientes:

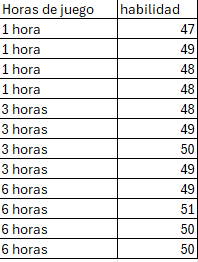
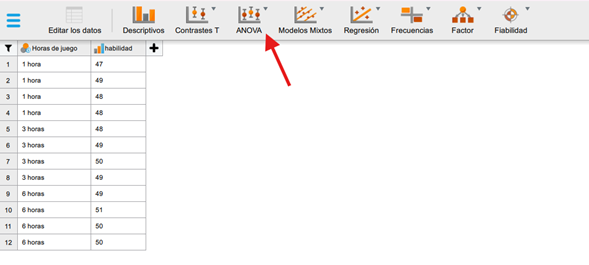
 Una vez cargados los datos en JASP(ver el siguiente enlace donde se explica dicho proceso https://siepsi.com.co/2024/04/12/como-y-cuando-hacer-una-prueba-t-para-muestras-pareadas/) debemos clicar en la pestaña de ANOVA como se muestra en la siguiente imagen:

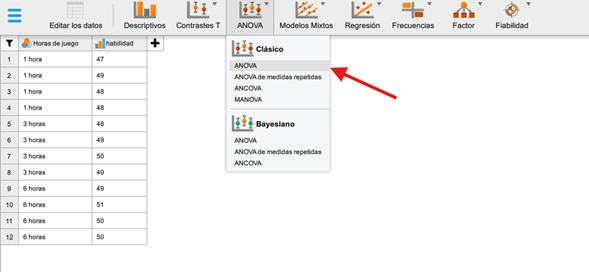
Después de esto clicar en ANOVA

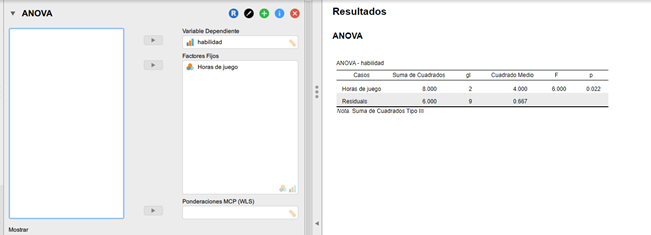
Una vez hecho esto debemos pasar nuestra variable de “habilidad” en la casilla de “variable dependiente” y nuestra variable “horas de juego” a la casilla de “factores fijos”

Después de esto vamos a buscar la pestaña de “verificación de supuestos” y vamos a clicar en el “contraste de homogeneidad”

Y obtendremos los siguientes valores:

Ahora ¿cómo debemos interpretar esta prueba de homogeneidad? Es muy sencillo, nuestra hipótesis nula nos dice que la varianza de nuestros datos es homogénea y nuestra hipótesis alternativa nos dice que nuestros datos son heterogéneos, sabiendo esto solo debemos interpretar el valor p de nuestros datos que en este caso es igual a 1, como este valor es igual o mayor que 0.05 podemos aceptar nuestra hipótesis nula.

Los siguientes pasos son igual de sencillos a los anteriores, una vez cumplido los supuestos los valores de nuestra ANOVA que ya habían aparecido antes nos arroja el siguiente resultado

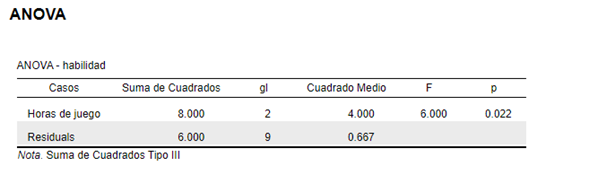
La interpretación en este punto es algo a tener en cuenta, debemos fijarnos en el valor p que en este caso es de 0.022 valor menor a 0.05 pero ¿qué podemos decir de esto? Tenga mucho cuidado en elegir la hipótesis nula y alternativa de una ANOVA ya que este valor no significa que hay diferencias significativas en las medias de todos los grupos, lo que realmente significa un valor menor o igual a 0.05 es que hay diferencias significativas en al menos UNA media de nuestros grupos, si buscamos en la pestaña “Contraste post-hoc” y pasamos nuestra variable “horas de juego” a la casilla de la derecha como se muestra en la imagen, podremos descubrir en cuál de nuestros grupos hay diferencias significativas

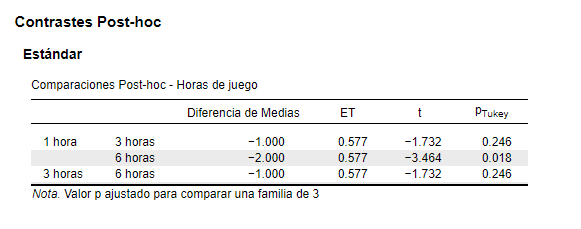
Ahora si nos fijamos en la p que aparece en los resultados, podemos ver que los grupos que presentan diferencias significativas son el grupo de 1 hora y de 6 horas de juego.

Como conclusión de este ejercicio podemos decir que rechazamos la hipótesis nula y aceptamos nuestra hipótesis alternativa, al menos en uno de nuestros grupos hay diferencias significativas en nuestras medias, específicamente, en el grupo de una hora y de seis horas de juego podemos ver una diferencia en la habilidad de los jugadores.

Ya sabemos entonces cómo y cuándo utilizar un análisis de varianza con muestras independientes de un solo factor; tenga en cuenta que, si sus datos tienen muestras dependientes o más de un factor, usted deberá implementar otros métodos o análisis para sus datos.

Bibliografía

Aron, A. y Aron E. 2001. Estadística para psicología. Pearson education.

Alfonzo Villegas Loazno. (4 de diciembre de 2022). ANOVA 1 FACTOR CON MUESTRAS INDEPENDIENTES (TEMA 5). DISEÑOS DE INVESTIGACIÓN Y ANÁLISIS DE DATOS. [Archivo de Video]. https://www.youtube.com/watch?v=37wBDWtp_uw

Pérez, H. 2008. Estadística para las ciencias sociales, del comportamiento y de la salud. Cengage Learning.

Pagano, R. 1999. Estadísticas para ciencias del comportamiento. Thomson.