Lo que Callan los Valores Perdidos
Por: Sebastián Castro Álvarez
marzo 30 del 2022
Uno de los muchos dolores de cabeza que existen cuando recolectamos y analizamos datos es la presencia de valores perdidos, y muchas veces, cuando nos enfrentamos a este problema, la solución más simple parece ser ignorarlos y eliminar filas enteras de datos. Sin embargo, ignorar los valores perdidos puede ser aún más problemático que su misma presencia ya que podemos estar omitiendo información relevante, estimando parámetros sesgados, perdiendo poder estadístico y haciendo inferencias incorrectas. En la entrada del día de hoy vamos a presentar algunos de los métodos estadísticos disponibles para tratar los valores perdidos. A continuación, vamos a:
- Presentar los mecanismos acerca de como se distribuyen los valores perdidos propuestos por Rubin (1976).
- Explicar brevemente los métodos de eliminación e imputación que se suelen usar para tratar los valores perdidos.
- Ejemplificar y comparar los diferentes métodos de manejo de valores perdidos con datos simulados.
- Dar una conclusión general y hacer recomendaciones para el lector.
Los Mecanismos de Rubin
Hay diversos motivos por los que podemos tener valores perdidos: Es posible que algunas personas hayan omitido por error algunas de las preguntas en un cuestionario; o si estamos haciendo un estudio longitudinal, es posible que algunas personas hayan abandonado el estudio después de un par de años. Incluso la opción de respuesta No sabe
no responde puede ser una fuente de valores perdidos. Pero hoy, lo que nos interesa es el cómo se presentan los valores perdidos, no el por qué. Para esto, Rubin (1976) propuso tres mecanismos que hacen supuestos acerca de la forma en la que se presentan y distribuyen los valores perdidos en nuestros datos. Específicamente, los mecanismos propuestos son: Valores perdidos completamente aleatorios (missing completely at random; MCAR), valores perdidos aleatorios (missing at random; MAR) y valores perdidos no aleatorios (missing not at random; MNAR). Estos tres mecanismos son discutidos y presentados frecuentemente en la literatura. Las definiciones que presento a continuación están basadas en De Leeuw et al. (2003) y Schafer & Graham (2002).
En primer lugar, tenemos MCAR, este mecanismo supone que los valores perdidos en nuestros datos se presentan de manera completamente aleatoria, es decir que no dependen ni de los valores observados en otras variables, ni del valor que se pudo haber observado en el caso de que el dato no se hubiera perdido. Si este supuesto se cumple, es posible ignorar los valores perdidos sin la preocupación de que vaya a haber un sesgo en los parámetros de interés. En la práctica, esto puede suceder cuando por ejemplo en una encuesta, algunos encuestados omiten algunas de las preguntas por error pero no de manera sistemática. En teoría, si estas omisiones no se deben al contenido de las preguntas o a ciertas características de los encuestados, se puede asumir que el mecanismo por el cual se distribuyen los valores perdidos es MCAR.
En segundo lugar, tenemos MAR, que supone que la distribución de los valores perdidos en nuestros datos se puede explicar por otras variables observadas. Por ejemplo, en un experimento, los participantes son citados para realizar el experimento en diferentes franjas horarias de manera aleatoria. Algunos, son citados en la mañana, otros en la tarde y
otros en la noche. Inevitablemente, algunos participantes no cumplieron con la cita al laboratorio, por lo cual hay valores perdidos una vez finalizada la recolección de datos. Después de revisar los datos, los investigadores notan que la mayoría de los valores perdidos es de participantes que fueron citados en la franja de la noche. De esta manera, la presencia de valores perdidos en los datos se puede explicar por el horario (variable observada) en el que fue citado el participante. A causa de esto, los investigadores de este estudio asumen que el mecanismo por el cual se distribuyen sus valores perdidos es MAR.
Finalmente, MNAR supone que la distribución de los valores perdidos se explica por el valor que estos valores pudieron tomar en el caso de que hubieran sido observados. En otras palabras, considerando por ejemplo un estudio en depresión que incluye pre-test, intervención y post-test, podríamos tener MNAR si las personas para quienes la intervención fue lo más efectiva deciden no ir al post-test porque ya se sienten muy bien. En este caso, la distribución de los valores perdidos se explicaría precisamente por los valores que no pudimos observar (es decir que efectivamente no son aleatorios) y es posible que concluyamos que la intervención es menos eficaz de lo que realmente es. Cabe aclarar que los mecanismos MCAR, MAR y MNAR son suposiciones teóricas acerca de la distribución de nuestros datos perdidos, pero realmente no podemos decir a ciencia cierta si nuestros valores perdidos se distribuyen de acuerdo a alguno de estos mecanismos. A pesar de que hay ciertos procedimientos que permiten analizar los patrones de los valores perdidos (De Leeuw et al., 2003), la suposición que hagamos acerca del mecanismo en el que se distribuyen los valores perdidos tiene que hacerse en combinación con la teoría, la lógica, los datos, y nuestro propio conocimiento acerca del fenómeno de interés. En la práctica, en la mayoría de investigaciones se suele asumir que los valores perdidos se distribuyen de acuerdo a MAR porque resulta más razonable asumir que los valores perdidos se pueden explicar por otras variables observadas frente a asumir que se presentan de manera completamente aleatoria y porque supone menos dificultades a la hora de manejar los valores perdidos que cuando se distribuyen de acuerdo a MNAR.
Tratando los Valores Perdidos
Y ¿Cómo puedo hacer mis análisis estadísticos cuando tengo valores perdidos? Bueno, para responder a esta pregunta vamos a presentar lo que se suele hacer pero que no se debería hacer, y lo que se debería hacer pero que rara vez se hace. En otras palabras vamos a hacer una breve revisión de los métodos estadísticos para el manejo de valores perdidos disponibles, haciendo la salvedad de que de los métodos expuestos solo recomendamos usar la imputación múltiple. Específicamente, a continuación vamos a presentar métodos de eliminación de datos, como són listwise y pairwise deletion, métodos de imputación simple y múltiple, y métodos de estimación por máxima verosimilitud. Cabe aclarar que los métodos presentados en este blog no son una lista exhaustiva de todos los métodos disponibles. Para mayores detalles sobre estos y otros métodos para el manejo de valores perdidos, recomiendo consultar Schafer & Graham (2002).
Métodos de Eliminación de Datos
La eliminación de datos es el método que se utiliza de manera predeterminada en la mayoría de los software y paquetes estadísticos. La eliminación de datos se suele hacer de dos maneras: Listwise o pairwise deletion. En la listwise deletion, cualquier fila que tenga al menos un valor perdido es eliminada de los análisis. En la pairwise deletion, las filas con valores perdidos se eliminan de manera diferencial dependiendo de las variables que se necesiten para el procedimiento que se va a implementar. Por ejemplo, consideremos la base de datos trees (disponible en R) que incluye el diámetro, la altura y el volumen de madera de 31 cerezos talados. Para hacer una pequeña demostración, incluí valores perdidos en todas las variables de la siguiente a manera:

La Tabla 1 muestra como quedarían los datos incompletos:
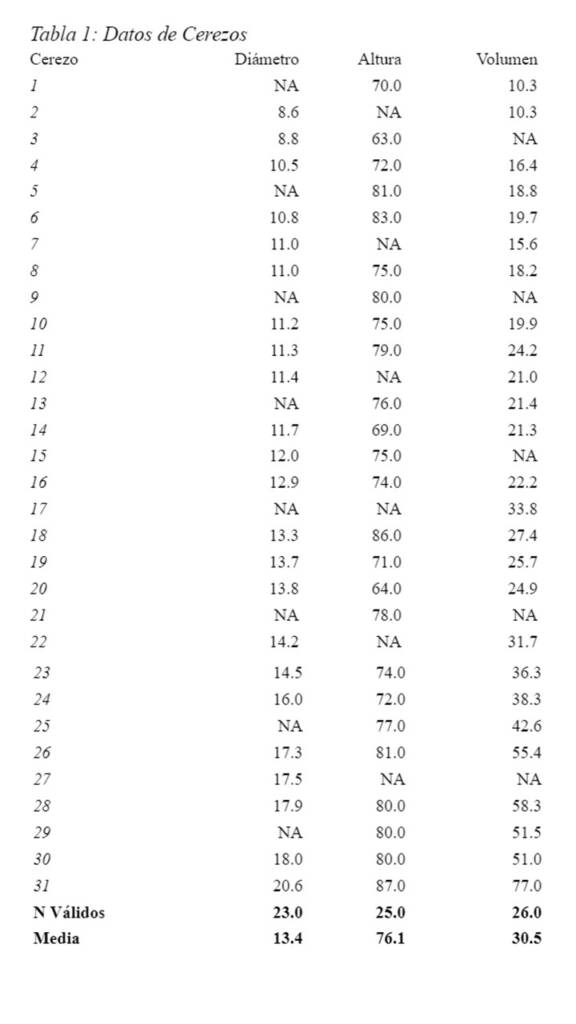
Si usáramos listwise deletion, eliminaríamos todas las filas en las que hay valores perdidos, esto reduciría la base de datos a sólo 16 casos válidos de 31. Por el contrario con pairwise deletion, la cantidad de casos válidos varía de acuerdo con el par de variables en el que estemos interesados. Así, si quisiéramos calcular la correlación entre diámetro y altura tendríamos 18 casos válidos, si quisiéramos estimar la correlación entre diámetro y volumen tendríamos 20 casos válidos, y si quisiéramos estimar la correlación entre altura y volumen tendríamos 21 casos válidos.
Estos métodos pueden resultar en estimados no sesgados si y solo si el mecanismo por el cual se distribuyen los valores perdidos es MCAR. Y aún así, no son recomendables porque al reducir el número de casos disponibles también se reduce el poder estadístico del procedimiento que queramos implementar.
Métodos de Imputación Simple
Una alternativa a eliminar e ignorar la presencia de los valores perdidos es la de asignarles valores probables. Una vez se le ha asignado (imputado) un valor probable a cada valor perdido, se asume que el valor imputado es el valor que hubiera sido observado y se analizan los datos como si se hubieran observado por completo. Pero ¿Cómo se calcula este valor probable? Por supuesto que hay infinidad de valores probables para cada valor perdido y a lo largo de los años se han propuesto una diversidad de métodos, algunos de los cuales explicamos a continuación, para hallar ese valor.
Imputación Simple: Media Incondicionada
El método de imputación simple más conocido es la imputación de la media que acá denominamos media incondicionada. En este método de imputación, a los valores perdidos se les asigna la media de los valores observados. Así, en la base de datos trees, a los valores perdidos en la variable Diámetro se les asignaría el valor de 13.4, que es la media de los casos válidos para esta variable; de igual forma, en la variable Altura se les asignaría el valor de 76.1; y en la variable Volumen se les asignaría el valor de 30.5.
A pesar de que la imputación incondicional de la media suele ser el método más conocido de imputación, este tampoco es recomendable. Este método puede ser útil para obtener estimados insesgados de medidas de tendencia central siempre y cuando el mecanismo por el cual se distribuyan los valores perdidos sea MCAR o MAR. Sin embargo, ya que este tipo de imputación no tiene en cuenta la dispersión de los datos, los valores estimados de las varianzas, covarianzas y de las relaciones entre las variables si estarán sesgados.
Imputación Simple: Media Condicionada
Otro método de imputación simple es el de la media condicionada. En este método se busca predecir los valores perdidos en una variable por medio de las otras variables observadas, generalmente con un modelo lineal. Por ejemplo, si deseamos imputar los valores perdidos en la variable Volumen, podemos ajustar un modelo de regresión lineal en el cual Volumen es la variable dependiente, y Diámetro y Altura son las variables independientes. El modelo de regresión lo ajustamos de la siguiente manera:

Así, para imputar, por ejemplo, el tercer dato de la variable Volumen, podemos reemplazar los valores observados y los coeficientes de regresión en la ecuación de regresión de la siguiente manera para calcular el valor ajustado de Volumen3:
Volumen3 =0+1*Diámetro3+2*Altura3, =-76.9+5.2*8.8+0.5*63, =-0.14.
Aquí vemos que, según este método, el valor que le deberíamos asignar al tercer dato de la variable Volumen es -0.14. Esto de entrada no es ideal, dado que el valor del volumen no debería ser negativo. Probablemente, se podría mejorar esta imputación al cambiar el modelo lineal por un modelo polinomial. En todo caso, de manera similar a la imputación de la media incondicionada, este método no es recomendable cuando se quieren estimar relaciones entre variables porque estas relaciones suelen sobrestimarse.
Imputación Simple: Distribución Incondicionada
Uno de los métodos que sí tiene en cuenta (hasta cierto grado) la distribución de los datos, es la imputación con distribución incondicionada, también conocida como hot deck. En este método de imputación, los valores perdidos se reemplazan con valores observados de manera aleatoria. Por ejemplo, volviendo al tercer valor de la variable Volumen, le podríamos asignar cualquiera de los otros valores que fueron observados en esta variable como por ejemplo 10.3 o 58.3. Una vez más, este método puede llegar a ser útil si el mecanismo por el cual se distribuyen los valores perdidos es MCAR o MAR y si uno esta interesado en estimar las medidas de tendencia central o medidas de dispersión de una variable. Sin embargo, si el interés es estudiar las relaciones entre las variables, este método tiende a sesgar y minimizar estas relaciones.
Imputación Simple: Distribución Condicionada
La imputación simple con distribución condicionada es el último método de imputación simple que vamos a discutir en este blog. Básicamente, este método es una mejora a la imputación simple con media condicionada porque en este caso, no se le asigna a los valores perdidos el valor ajustado por el modelo de regresión. En su lugar, se le asigna un valor aleatorio de la distribución condicional de la variable dependiente dadas las variables independientes. En otras palabras, se le adiciona error aleatorio (tomado de la distribución de los residuales) al valor ajustado. Retomando el ejemplo anterior, con la imputación del tercer dato de la variable Volumen, en este tipo de imputación no le asignaríamos un valor de -0.14, sino que a este valor le sumaríamos un valor aleatorio tomado de una distribución normal con media 0 y desviación estándar 3.85 y el resultado de esta suma sería el valor imputado.
Este método de imputación es capaz de estimar una gran variedad de parámetros poblacionales de manera insesgada siempre y cuando el mecanismo por el cual se distribuyen los valores perdidos sea MCAR o MAR y que el modelo estadístico haya sido especificado de manera correcta. Aún así, este método de imputación no tiene en cuenta la incertidumbre que existe alrededor de los valores perdidos, pues si bien el valor propuesto es probablemente adecuado, también podríamos encontrar otros cientos de valores probables si tomamos algún otro valor de la distribución de los residuales y se lo sumamos al valor ajustado.
Métodos de Imputación Múltiple
Como su nombre lo indica, la imputación múltiple consiste en proponer múltiples valores probables para cada valor perdido. Muchos de los métodos de imputación múltiple estan basados en los métodos de imputación simple como los de distribución condicionada e incondicionada. Así, con la imputación múltiple, se generan múltiples bases de datos completas que pueden ser analizadas de manera individual. Luego, los parámetros estimados para cada base de datos se combinan en un único valor estimado. Una de las mayores ventajas de estos métodos es que se tiene en cuenta la incertidumbre alrededor de los valores perdidos. Para esto, los algoritmos de imputación múltiple hacen una corrección de la varianza y de los intervalos de confianza. En general, se necesitan entre 10 y 20 imputaciones para obtener estimados insesgados (Schafer & Graham, 2002). La imputación múltiple es el método de imputación por excelencia. Este es el mejor método de imputación si el mecanismo por el cual se distribuyen los valores perdidos es MCAR o MAR. Para una descripción detallada de los procedimientos de imputación múltiple recomiendo consultar White et al. (2011).
Máxima Verosimilitud con Información Completa
Finalmente, los valores perdidos también se pueden tratar por medio de los métodos de estimación. Particularmente, la estimación por máxima verosimilitud con información completa permite estimar los parámetros de interés usando toda la información disponible. Este método suele estar disponible en software especializado para el análisis de ecuaciones estructurales como Mplus o lavaan. De la misma manera que los procedimientos de imputación múltiple, la estimación de máxima verosimilitud con información completa es un método adecuado para tratar los valores perdidos si el mecanismo por el cual se distribuyen es MCAR o MAR. También de manera similar, la incertidumbre que se tiene acerca de los valores perdidos se ve reflejada en el tamaño de los intervalos de confianza.
Manos a la Obra: Imputación en Acción
En esta tercera sección, voy a ejemplificar cómo usar cada método expuesto en la sección anterior (a excepción de la estimación por máxima verosimilitud con información completa) y cómo es su desempeño dado el mecanismo de distribución de los valores perdidos (MCAR, MAR, o MNAR) por medio de datos simulados. Para esto usaremos dos paquetes de R: MASS y mice. El primero nos permite simular datos con base en una distribución normal multivariada y el segundo permite implementar diferentes métodos de imputación simple y múltiple. La ventaja de usar datos simulados es que podemos saber con precisión cual es el valor poblacional de los parámetros de interés, por lo tanto, podemos saber que tan sesgado esta el parámetro estimado. Además, con datos simulados podemos saber cual el mecanismo real por el cual se distribuyen los valores perdidos. Para la simulación de los datos, consideremos que estamos interesados en la correlación de dos variables: Inteligencia y Atención. Inteligencia va a tener una media de 100 y una desviación estándar de 15, Atención va a tener una media de 50 y desviación estándar de 10, y la correlación real entre estas dos variables va a ser 0.6. Así, basados en estas distribuciones, vamos a simular datos para 100 individuos. Para esto vamos a utilizar la función mvrnom() del paquete MASS de la siguiente manera:

Los datos generados se presentan en la Figura 1 con su respectiva línea de regresión y coeficiente de correlación.
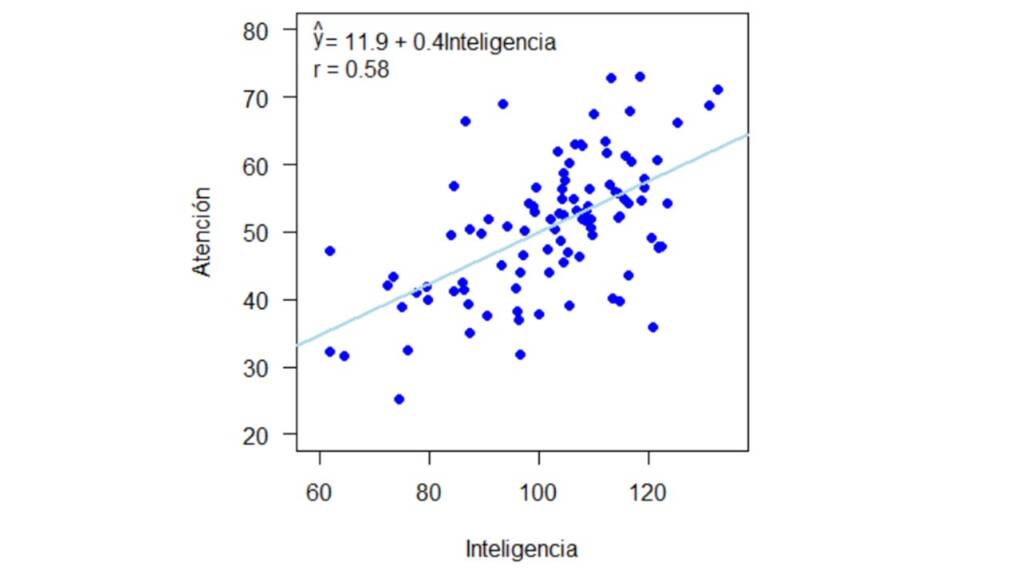
A continuación vamos a introducir valores perdidos en la variable Atención de acuerdo con cada uno de los tres mecanismos de valores perdidos y a comparar cómo cambia la estimación del coeficiente de correlación de acuerdo con cada una de los métodos para el manejo de valores perdidos.
MCAR
El primer mecanismo por el cual se distribuyen los valores perdidos es MCAR. Este es el mecanismo menos problemático pues los parámetros de interés se pueden llegar a estimar sin sesgo incluso con métodos de eliminación (es decir listwise o pairwise deletion). Supongamos que en la investigación en la que se recogieron estos datos, cada prueba era aplicada en días diferentes. Siendo que primero se hizo la evaluación de Inteligencia y luego se hizo la evaluación de Atención. Sin embargo, puede ser que cuando se citó a las personas para la evaluación en Atención, algunas no volvieron por razones desconocidas. Como consecuencia, sólo tenemos valores perdidos en la variable Atención y podemos asumir que se distribuyen de manera completamente aleatoria. Así, para incluir valores perdidos en la variable de Atención y para efectos de este ejemplo, vamos a asumir que la probabilidad de que una persona no atendiera la cita para la evaluación de Atención es de 0.4. Esto lo podemos hacer en R de la siguiente manera:

La Figura 2 muestra el gráfico con los datos completos a la izquierda y con los datos incompletos a la derecha. En ambos gráficos, adicioné la línea de regresión y el valor estimado de la correlación, que es nuestro parámetro de interés. Además, en el gráfico con los valores completos, resalté los valores perdidos en rojo. La línea de regresión y la correlación en el gráfico de la derecha serían nuestros resultados en caso de que usáramos un método de eliminación de los valores perdidos, que en este caso es listwise deletion.
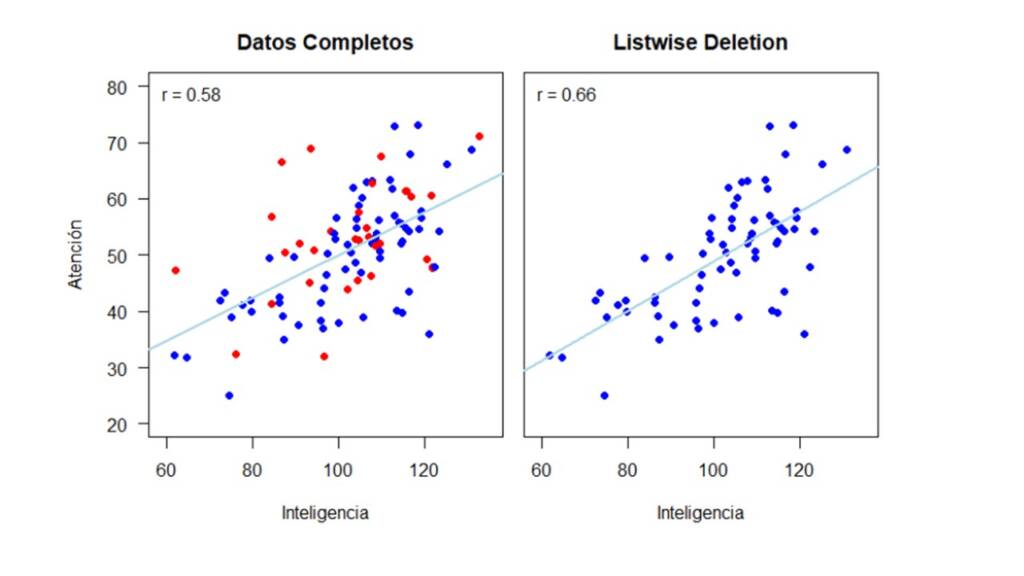
Ahora, vamos a imputar los valores perdidos, con cada uno de los métodos de imputación simple, es decir, por media y distribución condicionada e incondicionada. Esto lo podemos hacer con la función mice() que da como resultado un objeto de clase mids. Esta función permite usar diferentes métodos de imputación que son especificados por medio del argumento method. El número de imputaciones se define por medio del argumento m que en este caso es igual a 1. Luego, para acceder a la base de datos imputada podemos usar la función complete.

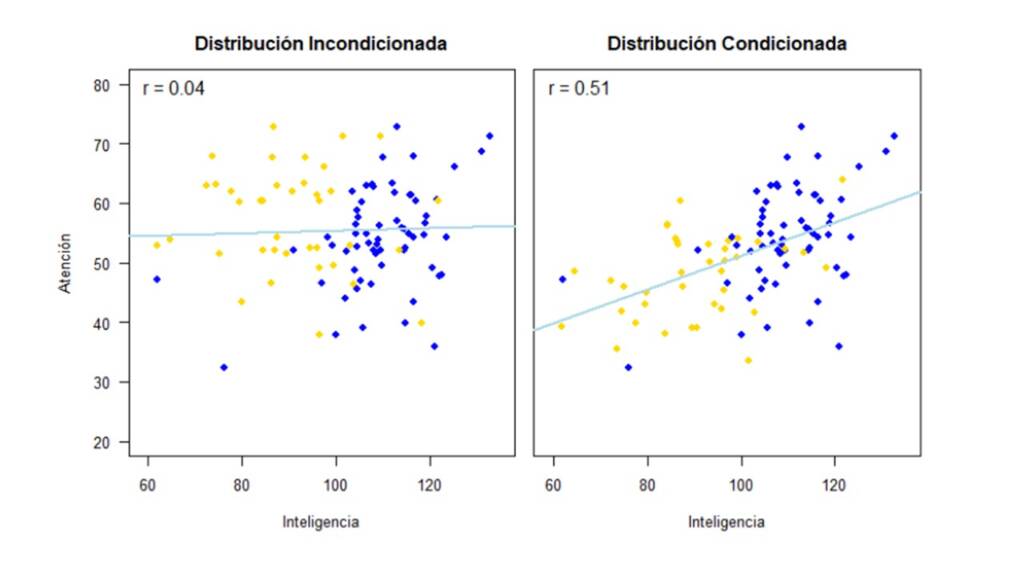
Los datos imputados por cada uno de los métodos con su respectiva línea de regresión y correlación estimada se muestran en la Figura 3. Los pares de valores observados están en color azul y los pares de valores para los cuales se imputó el valor en la variable Atención se resaltan en color amarillo.
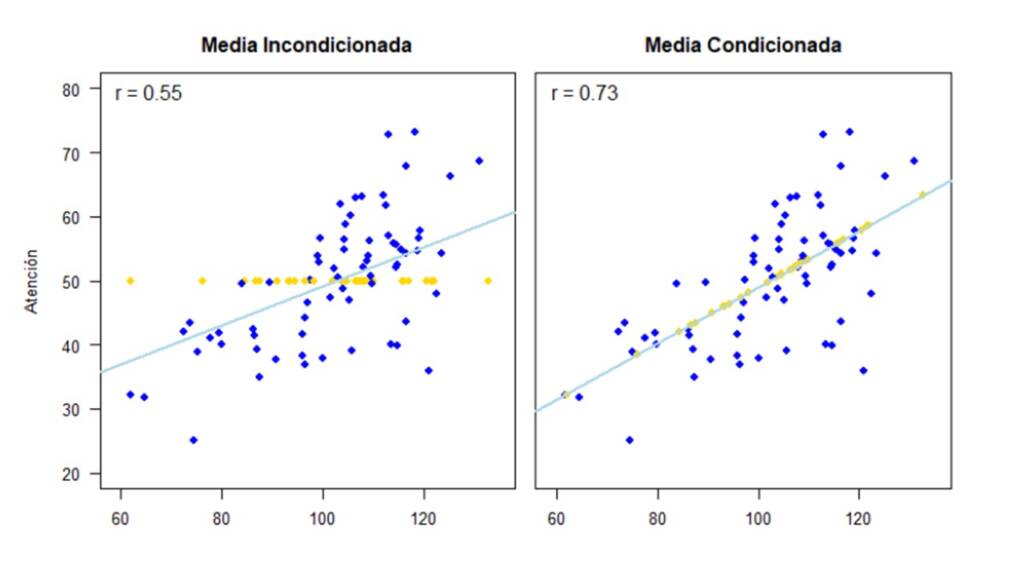
Por último, para la imputación múltiple, realizamos 15 imputaciones (m = 15) con el método norm, es decir, el mismo método que usamos para la imputación simple con distribución condicionada. Cabe aclarar que la función mice provee una gran variedad de métodos para la imputación múltiple y la selección de este depende de la naturaleza de las variables y el tipo de análisis que deseamos implementar. Adicionalmente, también podemos incluir otros argumentos en la función, como lo son: (a) El número de iteraciones maxit, para poder verificar la convergencia del algoritmo, y (b) la semilla aleatoria seed, para poder repetir los análisis con exactitud. Luego, con la función complete() podemos extraer las bases de datos imputadas. Como ahora tenemos múltiples datos imputados, adicionalmente tenemos que especificar si queremos acceder a una imputación en específico o a todas las diferentes imputaciones. Esto lo hacemos con el argumento action. Finalmente, lo que queremos hacer es repetir nuestros análisis con cada una de las bases de datos imputadas y combinar estos resultados. En concreto para nuestro ejemplo, tendríamos que estimar la correlación para cada una de las bases de datos imputadas y luego combinar las correlaciones estimadas en una única estimación. Todo esto lo podemos hacer con la función micombine.cor() del paquete miceadds. Para otros estadísticos de interés, como por ejemplo los coeficientes de regresión o medidas de tendencia central, son necesarias dos funciones del paquete mice: with() para analizar cada base de datos y la función pool() o pool.scalar() para combinar los resultados.

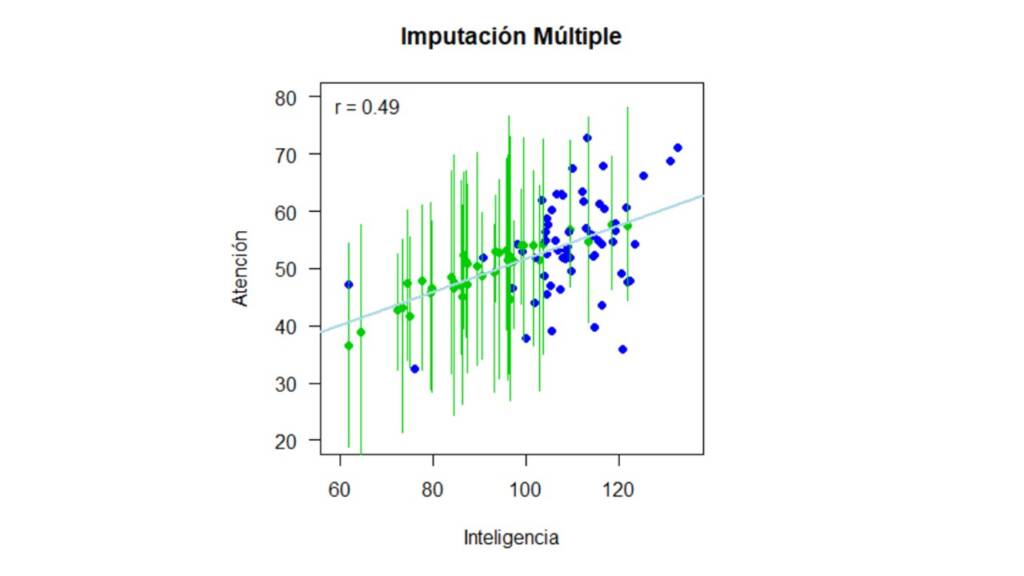
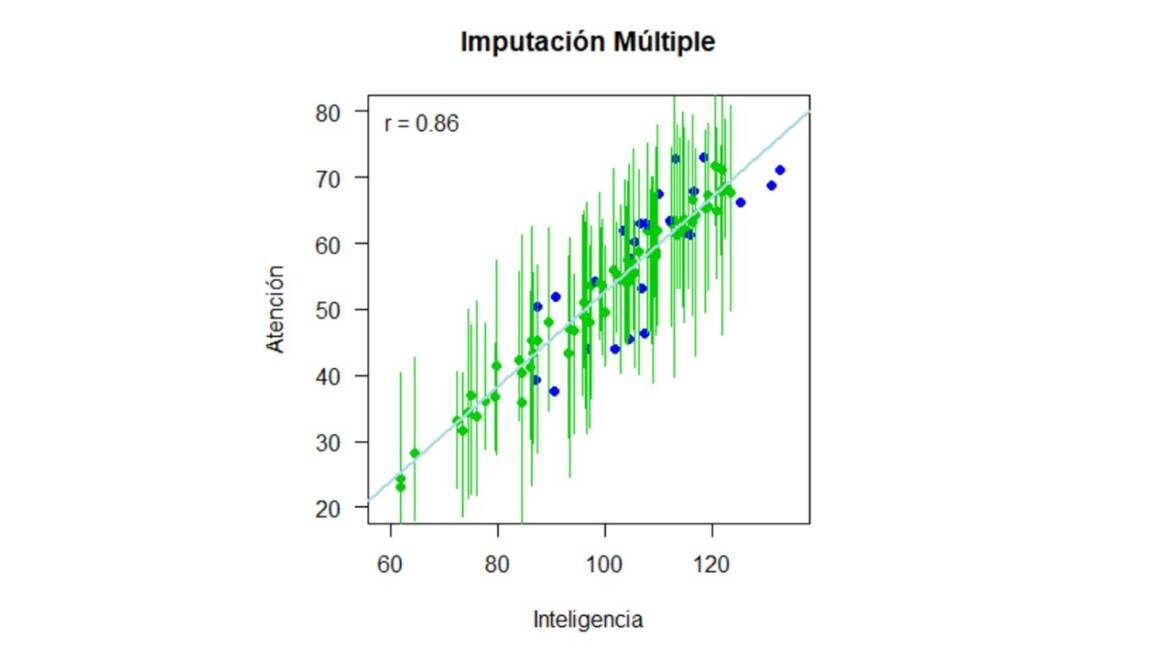
Un vez imputados los datos, podemos visualizarlos como se muestra en la Figura 4. En esta, los puntos verdes representan la media del valor imputado a través de las 15 imputaciones y los intervalos representan el rango del valor imputado. En otras palabras, si observamos el valor imputado que está más hacia la izquierda del gráfico, para la persona con un puntaje en inteligencia de 62, el intervalo verde indica que el menor puntaje imputado en la variable Atención para esta persona es de 23 y el mayor puntaje imputado es de 44.8.
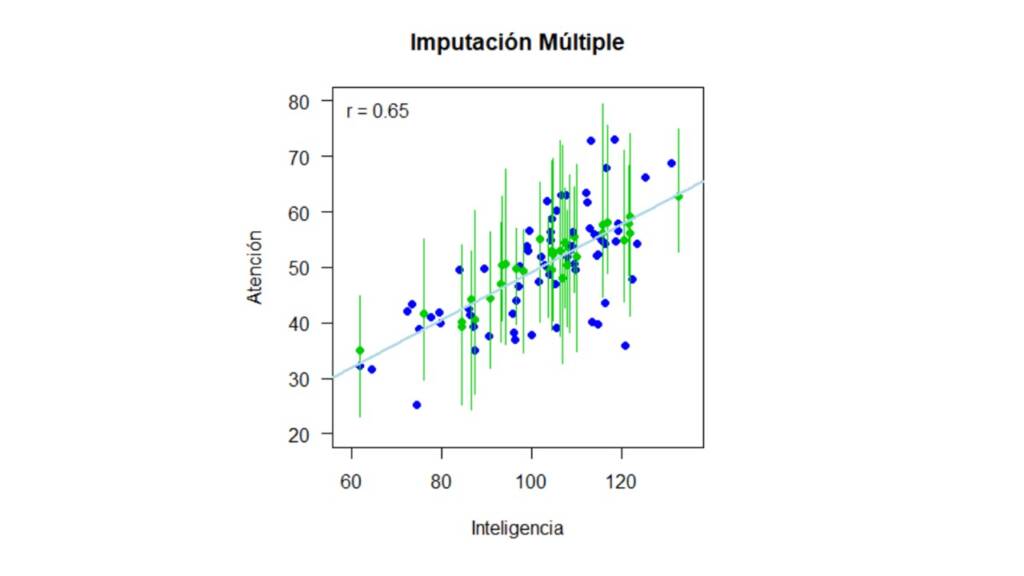
Comparando los resultados.
Ahora, para resumir toda la información anterior podemos poner en un gráfico la correlación estimada con su respectivo intervalo de confianza para cada método de la siguiente manera:
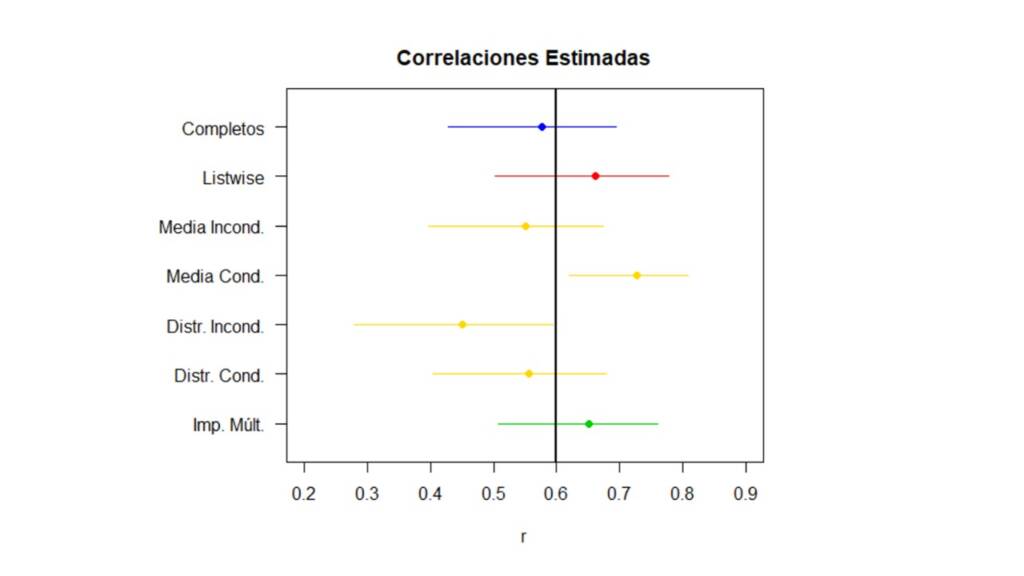
En la Figura 5, la línea vertical negra indica la correlación real entre las variables y el intervalo azul en la parte superior indica la correlación estimada y su intervalo de confianza cuando se utilizan los datos completos. Inmediatamente sobresalen por su pobre desempeño, la imputación simple con media condicionada y con distribución incondicionada. Esto no es ninguna sorpresa, pues ya sabíamos que la imputación con media condicionada fortalece artificialmente las relaciones entre las variables y que la imputación con distribución incondicionada debilita estas relaciones. Por el contrario los otros métodos no parecen diferir mucho, y cualquiera sería viable para manejar los valores perdidos de este ejemplo. Aunque estos resultados nos pueden hacer sentir optimistas acerca de los diferentes métodos, hay que tener en cuenta que esto solo es así porque el mecanismo real por el cual se distribuyen los valores perdidos es MCAR. Cuando este no es el caso, ya vamos a ver qué tan diferentes pueden llegar a ser los resultados.
MAR
Una segunda opción es que el mecanismo por el cual se distribuyen los valores perdidos sea MAR. Supongamos otra vez que las personas en este estudio eran citadas en dos días diferentes para responder a cada escala y se había decidido no citar para la evaluación de atención a las personas que quedaran catalogadas con discapacidad cognitiva de acuerdo con el puntaje de inteligencia. Sin embargo, la persona encargada de llamar a los participantes para agendar la segunda cita no tenía muchos conocimientos acerca de las escalas de inteligencia y pensó que las personas con puntajes menores de 100 tenían una deficiencia cognitiva, por lo cual no los citó para la evaluación en atención. Y además de no saber de escalas de inteligencia, también hizo las llamadas de afán y terminó llamando a unas pocas personas con puntajes menores de 100 en la escala de inteligencia y no llamando a otras que si debía llamar. ¡Un desastre!, ¡no sé cómo pudieron contratar a alguien así para hacer las llamadas! En todo caso, para introducir valores perdidos y para efectos de este ejemplo, le vamos a dar una probabilidad de 0.8 de tener un valor perdido en Atención a las personas con un puntaje en inteligencia menor a 100, y una probabilidad de 0.2 en caso contrario. Esto lo podemos hacer de la siguiente manera:

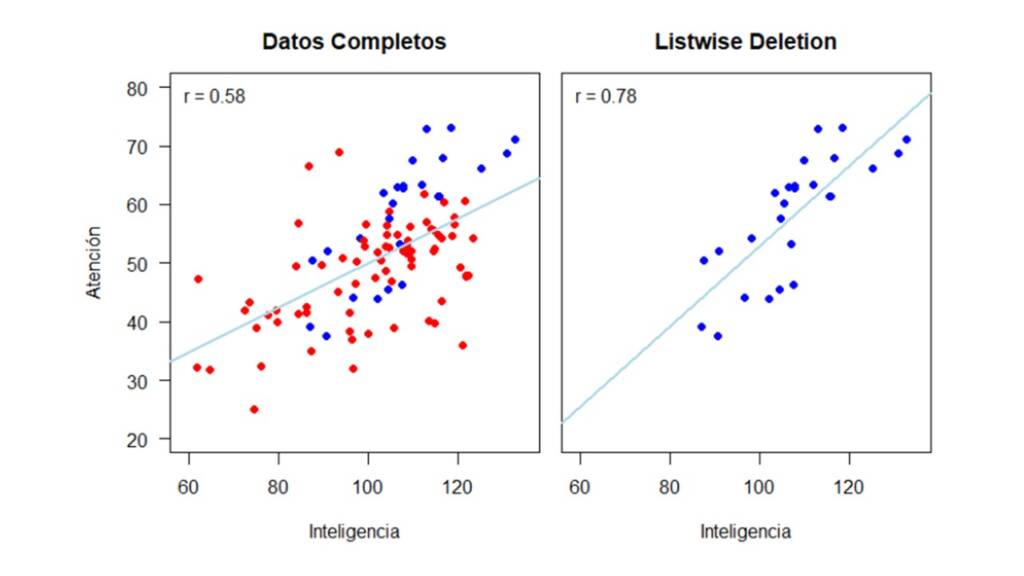
De igual manera que en la sección anterior, a continuación, mostramos cómo cambia la relación entre Inteligencia y Atención dependiendo de si se eliminan los casos con datos perdidos o si se utilizan métodos de imputación simple o múltiple. En la Figura 6 se muestra como la relación entre las variables cambia drásticamente al eliminar los casos con valores perdidos en la variable Atención. La correlación con los datos completos es de 0.58 y se disminuye a 0.4 cuando se utiliza listwise deletion.
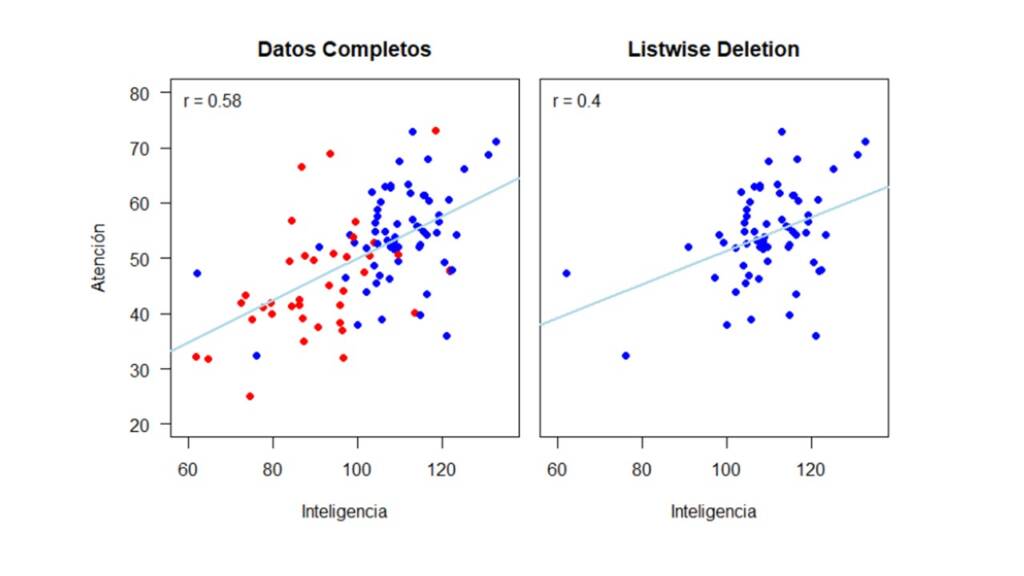
Por lo anterior, notamos como utilizar un método de eliminación no es conveniente para los propósitos del estudio cuando el mecanismo real por el cual se distribuyen los datos es MAR. Frente a esto, exploremos si los métodos de imputación simple se desempeñan mejor. Una vez más, usemos la función mice() para imputar los datos como se muestra en el siguiente código, que es básicamente el mismo código que usamos en la sección anterior pero usando la base de datos datos_mar en vez de datos_mcar.

Ya con los datos imputados, podemos observar en la Figura 7 como cambia la correlación entre las variables de acuerdo a cada uno de los métodos.
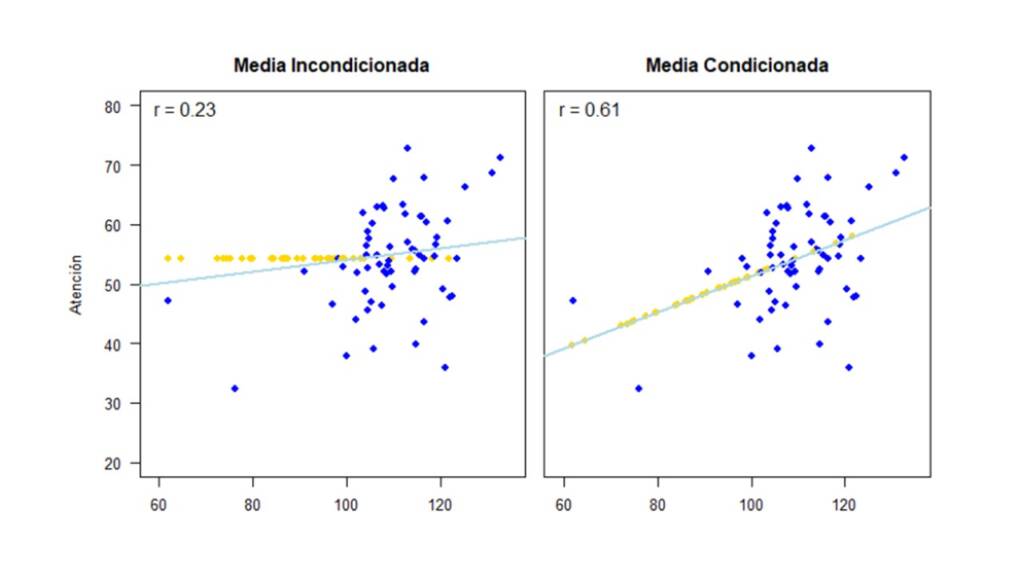
Y podemos hacer exactamente lo mismo para la imputación múltiple. En el código usamos datos_mar en vez de datos_mcar para hacer la imputación y en la Figura 8 mostramos el rango que los valores imputados.

Comparando los resultados.
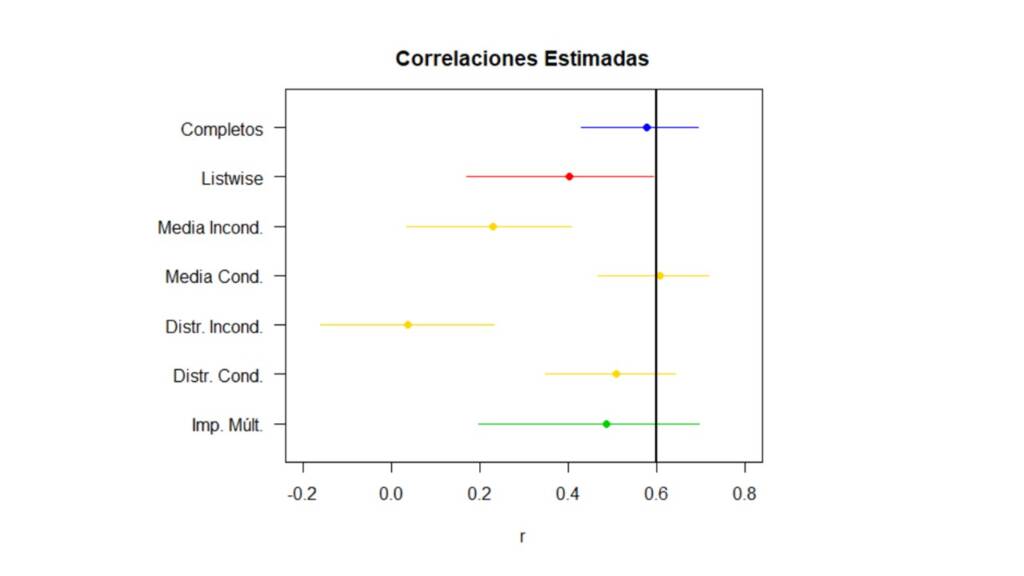
Ahora, para comparar fácilmente el desempeño de cada método, la Figura 9 presenta las correlaciones estimadas de acuerdo a cada método con sus respectivos intervalos de confianza. Así, se puede ver que, si el mecanismo por el cual se distribuyen los valores perdidos es MAR, usar un método de eliminación (listwise deletion) o métodos de imputación simple con media o distribución incondicionada subestima la correlación, por lo cual podríamos concluir erróneamente que Inteligencia y Atención no están relacionadas. Por el contrario, con la imputación simple con media o distribución condicionada y con la imputación múltiple, obtenemos una estimación de la correlación mucho más cercana a la correlación estimada con los datos completos. Notemos, que a pesar de que el intervalo de confianza obtenido por medio de la imputación múltiple es el más amplio de todos los intervalos de confianza, los resultados obtenidos por medio de este método son lo que tienen mayor validez ya que tienen en cuenta la incertidumbre acerca de los valores perdidos.
MNAR
Para finalizar, observemos que pasaría si el mecanismo por el cual se distribuyen los valores perdidos es MNAR. En este caso, los valores perdidos están directamente relacionados con el valor que hubiera sido observado en caso de que el dato no se hubiera perdido. Para nuestro ejemplo, supongamos que las dos pruebas fueron administradas de manera virtual, las personas primero respondían la prueba de inteligencia y al final de esta prueba había un pequeño botón que dirigía a las personas a la prueba de atención. Pues resulta que este botón era muy pequeño y fácil de pasar por alto. De esta manera, fue más probable que las personas con menores niveles de atención pasaran por alto el botón y no respondieran la siguiente prueba. Es decir, el hecho de que una persona no hubiera contestado la prueba de atención esta directamente relacionado con el nivel de atención de la persona. Así, en este ejemplo, le vamos a dar una probabilidad de 0.8 de tener un valor perdido a las personas con un puntaje en Atención menor a 60 y de 0.2 en caso contrario.

La Figura 10 muestra cómo se verían los datos y cuál sería la correlación estimada si usamos un método de eliminación.
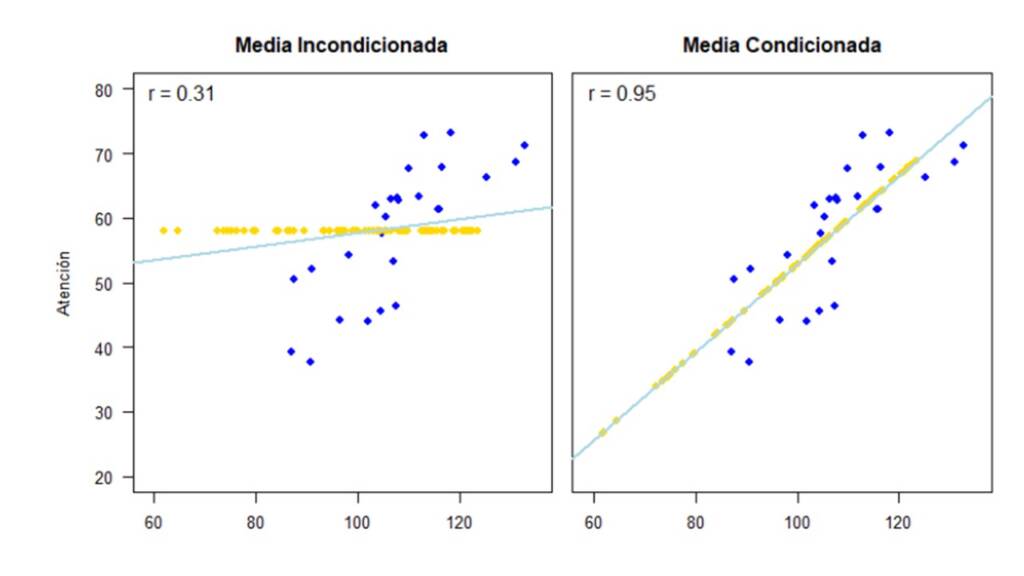
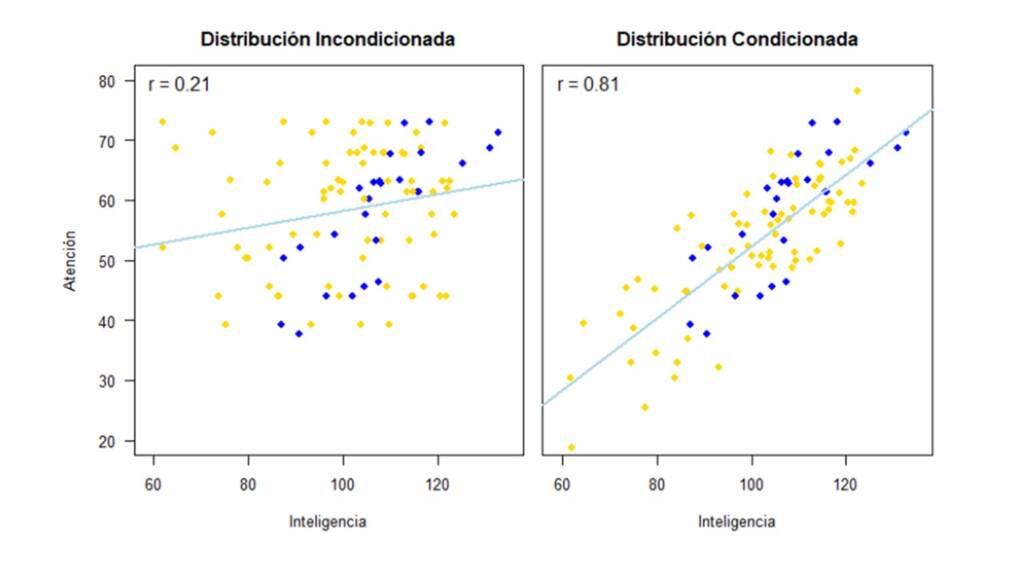
Si por el contrario utilizamos los métodos de imputación simple (el mismo código pero con la base de datos datos_mnar) tenemos como resultado los gráficos de dispersión y correlaciones que se presentan en la Figura 11.

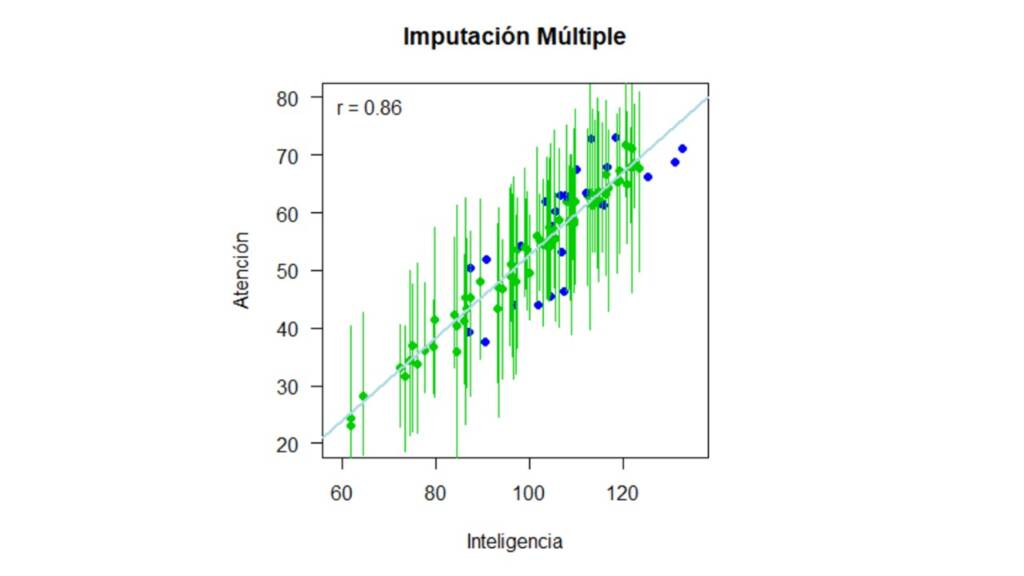
Por último, la Figura 12 muestra los resultados que obtenemos al utilizar imputación múltiple.

Comparando los resultados.
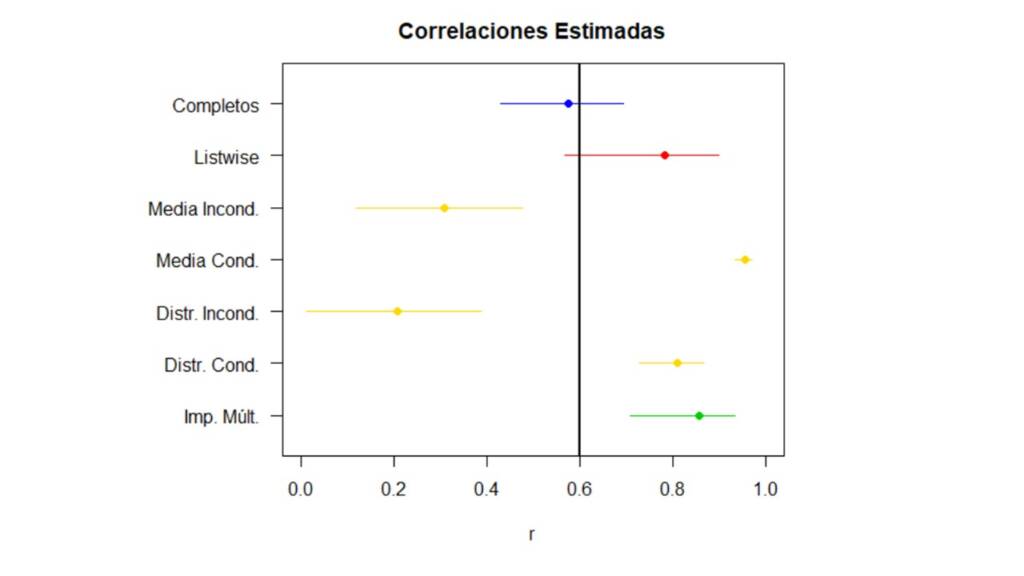
Cuando ponemos todas las correlaciones con sus intervalos de confianza en una única gráfica (ver Figura 13), vemos cómo todos los métodos tienen resultados completamente sesgados cuando el mecanismo por el cual se distribuyen los valores perdidos es MNAR. En este caso, ni siquiera la imputación múltiple puede dar un buen resultado.
Conclusiones y Recomendaciones
En este blog, expusimos brevemente los mecanismos de Rubin (1976) y algunos de los métodos más populares para el manejo de los valores perdidos. Por medio de un ejemplo, mostramos cómo estos métodos se desempeñan de maneras diferentes dependiendo de cuál es el mecanismo real por el cual se distribuyen los valores perdidos. El mensaje más importante que queríamos dar es que hay que pensar dos veces antes de usar los métodos de eliminación para manejar los valores perdidos y que es importante explorar los datos y tratar de inferir cuál es el mecanismo por el cual se distribuyen los valores perdidos (MCAR, MAR o MNAR).Como vimos en el ejemplo, los métodos de eliminación sólo proveen estimaciones no sesgadas si el mecanismo por el cual se distribuyen los valores perdidos es MCAR, y aun así usar estos métodos es un riesgo pues al disminuir el tamaño de la muestra, se disminuye la potencia estadística. Por el contrario, los métodos de imputación pueden conducir a resultados insesgados sin perder la potencia estadística tanto si el mecanismo por el cual se distribuyen los valores perdidos es MCAR o MAR. Así, ¿Qué método de imputación se debería usar? En general, la recomendación es que si se van a imputar los valores perdidos, el método por excelencia es la imputación múltiple. En el ejemplo, usamos la imputación múltiple con el método norm, sin embargo, la selección del algoritmo depende de la naturaleza de las variables y del tipo de análisis que se quiere realizar. Adicionalmente, una de las mayores ventajas de los métodos de imputación múltiple es que se tiene en cuenta la incertidumbre alrededor de los valores imputados. Es decir, como hay infinidad de valores probables para cada valor perdido, hacer una única imputación de este valor es asumir que si el valor no se hubiera perdido entonces hubiéramos observado, en efecto, el valor que estamos imputando. Esta suposición es demasiado determinista teniendo en cuenta que la imputación básicamente es una fabricación artificial de los datos faltantes. Así, cuando se hace la imputación múltiple, se reconoce que desconocemos cuál es el valor que se hubiera observado en caso de que no se hubiera perdido.
Finalmente, vimos que si el mecanismo por el cual se distribuyen los valores perdidos es MNAR, ninguno de los métodos presentados en este blog es adecuado para realizar los análisis de interés. Si se sospecha que los valores perdidos se distribuyen MNAR sería necesario buscar otros métodos en la literatura especializada o contactar de nuevo a los participantes con el fin de recolectar la información faltante. Aunque a decir verdad, en muchas ocasiones, uno como investigador solo está cruzando los dedos para que sus valores perdidos no se distribuyan MNAR.
Postdata: Al lector curioso, le propongo replicar los análisis del ejemplo acerca de la relación entre Inteligencia y Atención pero para estimar la media de Atención o los coeficientes de la regresión entre las dos variables.
Bibliografía
De Leeuw, E. D., Hox, J. J., & Huisman, M. (2003). Prevention and treatment of item nonresponse. Journal of Official Statistics, 19, 153-176.
Rubin, D. B. (1976). Inference and missing data. Biometrika, 63(3), 581-592. https://doi.org/10.1093/biomet/63.3.581
Schafer, J. L., & Graham, J. W. (2002). Missing data: our view of the state of the art. Psychological methods, 7(2), 147-177. https://doi.org/10.1037/1082-989X.7.2.147White, I. R., Royston, P., & Wood, A. M. (2011). Multiple imputation using chained equations: issues and guidance for practice. Statistics in medicine, 30(4), 377-399. https://doi.org/10.1002/sim.4067























Add Comment