Funcionamiento diferencial de los ítems (DIF)

.

Por: Cristian Stiven Tarapues Calpa

Como campo fundamental en psicología y educación, la psicometría ha revolucionado la forma en que medimos y evaluamos los constructos psicológicos. Este campo, surgido a principios del siglo XX proporciona la base teórica y metodológica para medir variables psicológicas que, por su naturaleza, no pueden ser observadas directamente (Muñiz, 2018). Hoy en día, la psicometría se ha convertido en una herramienta esencial para asegurar la confiabilidad y las evidencias de validez de las mediciones que se realizan en una variedad de campos y contextos.

Dentro de la Psicometría se cuenta con un concepto importante: el funcionamiento diferencial de los ítems (DIF por sus siglas en inglés). El DIF se presenta cuando individuos de diferentes grupos  que tienen los mismos niveles de la característica medida difieren en la probabilidad de respuesta correcta a un ítem debido a variables como género, cultura o etnia (Hidalgo y Gómez-Benito, 2010). Este concepto representa uno de los mayores desafíos en el diseño y validación de instrumentos, ya que  afecta directamente la validez y equidad de la medición. 

Teniendo en cuenta este marco referencial, es fundamental considerar la importancia del análisis DIF en la medición estandarizada y en la construcción de instrumentos, especialmente en un mundo cada vez más diverso y globalizado, en el cual este análisis se convierte en una herramienta esencial para identificar y eliminar posibles fuentes de desigualdad en los instrumentos de medición.

Diferencia entre DIF y Sesgo de ítems

Es fundamental distinguir entre el Funcionamiento Diferencial de los Ítems (DIF) y el sesgo de los ítems, dado que, aunque están relacionados, representan conceptos distintos dentro del análisis de pruebas, a saber:

Funcionamiento Diferencial de los Ítems (DIF): El DIF es un concepto estadístico que refleja diferencias en las propiedades psicométricas de un ítem entre grupos, estas diferencias se detectan a través de métodos analíticos, como el análisis de Mantel-Haenszel, regresiones logísticas o modelos de Teoría de Respuesta al Ítem (TRI) (Hidalgo y Gómez-Benito, 2010). En términos simples, el DIF indica que un ítem puede estar midiendo de manera diferente para subgrupos específicos, a pesar de que los individuos de ambos grupos tengan el mismo nivel en el constructo que se pretende medir.

Sesgo de los Ítems: Se trata del análisis que se realiza al contenido y la validez del ítem que explica las diferencias en su funcionamiento, las cuales se deben a características irrelevantes para el constructo que se mide. Dicho de otro modo, un ítem sesgado introduce inequidad al evaluar aspectos ajenos al objetivo de la prueba (Camilli y Shepard, 2014).

Por ende, comprender la relación entre la presencia de DIF y el sesgo resulta crucial, la existencia de DIF indica de forma cuantitativa la diferencia en la probabilidad de acierto, que se considera evidencia de sesgo cuando se demuestra que las diferencias en su funcionamiento no están relacionadas con el constructo que se pretende medir.

Para entender cómo opera el funcionamiento diferencial del ítem (DIF) en las evaluaciones colombianas, pensemos en una pregunta de opción múltiple típica de la prueba Saber 11 de comprensión lectora:
«Lea el siguiente fragmento de un cuento y seleccione la respuesta correcta.
¿Cuál es la enseñanza principal que transmite la historia sobre la importancia del café en la vida campesina colombiana?
A) El café representa la única fuente de ingresos para las familias rurales.
B) El cultivo del café fomenta la solidaridad y el trabajo colectivo en el campo.
C) El café impide que los jóvenes migren a las ciudades en busca de empleo.
D) El consumo excesivo de café afecta la salud de los campesinos.»

A primera vista, el ítem solo pide interpretar un texto; sin embargo, su temática introduce una diferencia silenciosa entre los estudiantes, quienes viven en el Eje Cafetero (Caldas, Risaralda y Quindío) han crecido rodeados de referencias al cultivo del café, su vocabulario y su valor sociocultural. Es probable que, incluso con la misma habilidad global de comprensión lectora, tengan mayor facilidad para inferir que la opción B es la adecuada, en comparación con compañeros de grandes urbes como Bogotá o Barranquilla. Al aplicar métodos estadísticos de detección de DIF, esa ventaja contextual suele traducirse en una probabilidad significativamente más alta de acierto para el grupo familiarizado con la cultura cafetera.
¿Podemos llamar sesgo a esta diferencia? Solo si contradice el propósito declarado de la prueba. Si lo que se busca es medir comprensión lectora «descontextualizada», centrada exclusivamente en habilidades de análisis textual, entonces la familiaridad cultural constituye un factor ajeno al constructo y el ítem resulta sesgado. En tal caso habría que modificar o sustituir la pregunta, o bien equilibrar el banco de ítems con temáticas representativas de otras regiones. Por el contrario, si la evaluación pretende valorar la capacidad de leer e interpretar textos enmarcados en la diversidad cultural colombiana, la ventaja deja de ser un sesgo y pasa a reflejar diferencias reales en experiencias lectoras.

Tipos de DIF

En el análisis del Funcionamiento Diferencial de los Ítems, se identifican dos tipos principales: el DIF uniforme y el DIF no uniforme (Swaminathan y Rogers, 1990). Cada uno representa un patrón distinto de funcionamiento diferencial que requiere diferentes aproximaciones para su detección y tratamiento. La distinción entre estos tipos es fundamental para comprender cómo los ítems pueden funcionar de manera diferente para distintos grupos y cómo esto puede afectar la validez de las pruebas.

DIF Uniforme

El DIF uniforme, también conocido como DIF consistente, ocurre cuando la diferencia en la probabilidad de respuesta correcta entre los grupos es constante a lo largo de todos los niveles del rasgo medido (Swaminathan y Rogers, 1990). En otras palabras, un grupo sistemáticamente tiene mayor probabilidad de responder correctamente al ítem que el otro grupo, independientemente del nivel de habilidad.

Como ejemplo consideremos un ítem de comprensión lectora que incluye vocabulario específico de un contexto urbano, en este caso, los estudiantes de zonas urbanas podrían tener consistentemente una mayor probabilidad de responder correctamente que los estudiantes de zonas rurales, sin importar su nivel real de comprensión lectora, la ventaja del grupo urbano probablemente se mantendrá constante en todos los niveles de habilidad.

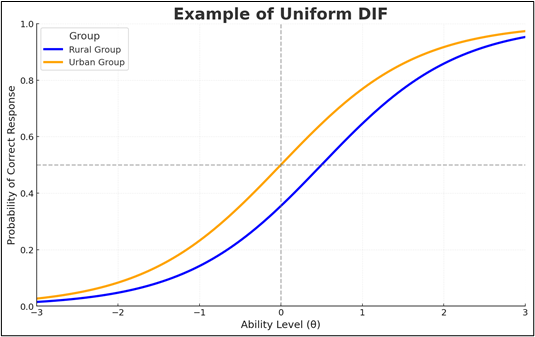
En este ejemplo, las dos curvas representan a dos grupos distintos:

• Curva naranja: Estudiantes de zonas urbanas.
• Curva azul: Estudiantes de zonas rurales.

El eje x muestra el nivel de habilidad (θ) de los participantes, que varía de valores bajos a altos. El eje y indica la probabilidad de que un participante de un grupo específico responda correctamente al ítem.

Interpretación de la gráfica:

• Habilidad baja (θ < −1.5): la curva del grupo urbano (naranja) está por encima del grupo rural (azul) de forma consistente; el grupo urbano tiene mayor probabilidad de acierto incluso en niveles bajos.
• Habilidad media (−1.5 ≤ θ ≤ 1.5): la ventaja del grupo urbano se mantiene prácticamente con la misma separación; no hay cruces ni cambios de dirección.
• Habilidad alta (θ > 1.5): ambas curvas se acercan al techo, pero el grupo urbano sigue por encima; la ventaja persiste aunque la brecha pueda reducirse por saturación.

La diferencia entre grupos es estable en todo el continuo de habilidad (no depende de θ), eso es exactamente lo que llamamos DIF uniforme. Este tipo de sesgo puede ocurrir cuando el ítem favorece sistemáticamente a un grupo debido a factores externos, como un contexto cultural o lingüístico, como se ilustra en el ejemplo se beneficia al grupo urbano frente al grupo rural.

DIF No Uniforme

El DIF no uniforme o DIF cruzado se presenta cuando la diferencia en la probabilidad de respuesta correcta entre los grupos varía según el nivel del rasgo medido (Swaminathan y Rogers, 1990). En este caso, la ventaja de un grupo sobre otro cambia o incluso se invierte dependiendo del nivel de habilidad, lo que causa que la probabilidad de éxito en el ítem varíe de manera diferente entre los grupos a lo largo de los niveles de habilidad. Para ejemplificar, imaginemos un problema matemático que requiere conocimientos de física: “Un automóvil viaja a 60 km/h. Si aumenta su velocidad en un 25% durante 45 minutos, ¿qué distancia adicional recorrerá comparada con su velocidad inicial”. Este problema combina habilidades matemáticas (cálculos de porcentajes, conversión de unidades y resolución de problemas) con conocimientos de física (entender cómo la velocidad y el tiempo se relacionan con la distancia). Aquí, el DIF No Uniforme se refiere a que el desempeño en este problema varía de manera desigual entre grupos de estudiantes, dependiendo de su nivel de habilidad matemática y su formación en física.

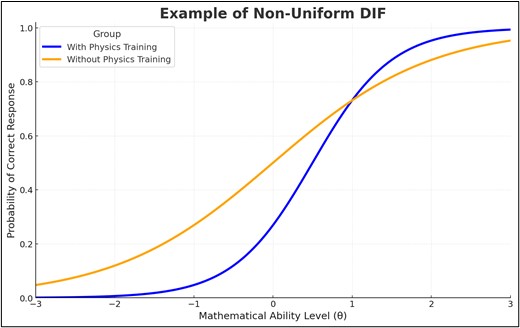
En este ejemplo, las dos curvas representan a dos grupos distintos:

• Curva azul: Grupo con formación en física.
• Curva naranja: Grupo sin formación en física.

Interpretación de la gráfica:

• Cruce de curvas (punto de no-uniformidad): Las curvas se igualan y cruzan cerca de θ ≈ 0.9–1.0, con una probabilidad ~0.73 para ambos grupos. Ahí no hay ventaja neta.
• Niveles bajos de habilidad (θ < 0): El grupo sin formación en física (naranja) presenta probabilidades claramente mayores. Ej.: en θ = −1, naranja ≈ 0.26 vs. azul ≈ 0.05 (ventaja de ~0.21).
• Transición a media habilidad (0 ≤ θ < 1): La ventaja naranja disminuye progresivamente a medida que aumenta θ hasta desaparecer en el cruce (~0.9–1.0).
• Niveles medios-altos (1 < θ ≤ 2): Tras el cruce, el grupo con formación en física (azul) supera al naranja y la brecha crece con θ. Ej.: en θ = 2, azul ≈ 0.96 vs. naranja ≈ 0.88 (ventaja ~0.08 a favor de azul).
• Niveles muy altos (θ > 2): Ambas curvas se acercan al techo (≈1.0), por lo que la diferencia se estrecha de nuevo por efecto de saturación.

El DIF no uniforme ocurre cuando la ventaja entre grupos varía a lo largo del nivel de habilidad (θ). No significa siempre que las curvas deban cruzarse, aunque el gráfico 2 sea un caso muy ilustrativo: puede que un grupo tenga mejor desempeño en niveles bajos y el otro en niveles altos, o que la diferencia entre ellos se amplíe o reduzca conforme aumenta la habilidad. En nuestro ejemplo, el ítem favorece al grupo sin formación en física en niveles bajos, pero a medida que la habilidad matemática crece, la ventaja se invierte y pasa al grupo con formación en física. Esto muestra que el desempeño relativo depende del nivel de θ y no es constante, lo que caracteriza al DIF no uniforme.

Métodos para detectar el DIF

Técnicas Clásicas

Las técnicas clásicas para la detección del DIF representan los primeros métodos desarrollados y ampliamente utilizados en la práctica psicométrica, estas técnicas se caracterizan por su relativa simplicidad computacional y su robustez en la aplicación práctica.

Análisis de Mantel-Haenszel

El método de Mantel-Haenszel (MH), introducido en el contexto del análisis de DIF por Holland y Thayer (1988), es uno de los procedimientos más utilizados en evaluación educativa gracias a su sencillez, eficacia y solidez estadística. Este enfoque permite comparar la probabilidad de que diferentes grupos respondan correctamente un ítem, controlando por el nivel global de habilidad, con el fin de detectar posibles sesgos en el funcionamiento de las preguntas.

El método se basa en la distinción entre dos grupos clave:

Grupo de referencia: según Holland y Thayer (1988) este grupo actúa como punto de comparación. Está compuesto por los estudiantes que, teóricamente, no enfrentan desventajas culturales, lingüísticas o contextuales con respecto al contenido del ítem. Se asume que para este grupo el ítem funciona de manera neutral.

Grupo focal: también definido por Holland y Thayer (1988), este grupo incluye a los estudiantes que podrían estar en desventaja o ventaja frente al ítem, por razones que no están directamente relacionadas con la habilidad que se pretende medir (por ejemplo, una familiaridad cultural o temática que facilita la respuesta correcta).

Una vez definidos los grupos, el método MH compara sus respuestas correctas en cada nivel de habilidad utilizando tablas de contingencia. A partir de ahí, calcula un estadístico chi-cuadrado para evaluar si la diferencia observada es significativa, además, ofrece una medida del tamaño del efecto que permite clasificar el grado de DIF observado. Por ejemplo, según los criterios del Educational Testing Service (ETS), los ítems pueden clasificarse como de DIF negligible, moderado o grande, lo que orienta decisiones sobre su permanencia o modificación.

Principales características del método Mantel-Haenszel:

• Eficaz para detectar DIF uniforme (cuando la ventaja o desventaja se mantiene constante en todos los niveles de habilidad).
• Utiliza tablas de contingencia para controlar por habilidad general.
• Proporciona un estadístico chi-cuadrado para evaluar la significación estadística.
• Incluye un índice de tamaño del efecto, que permite interpretar el impacto práctico del DIF.
• Es ampliamente utilizado por organismos de evaluación debido a su confiabilidad y bajo requerimiento computacional.

En síntesis el método de Mantel-Haenszel permite identificar ítems que funcionan de forma distinta entre grupos con igual habilidad y su implementación clara y sus criterios bien establecidos lo convierten en una herramienta clave para desarrolladores de pruebas interesados en asegurar la validez.

Métodos de Regresión

Los métodos de regresión logística representan una aproximación más flexible para la detección del DIF, capaz de identificar tanto DIF uniforme como no uniforme (Swaminathan y Rogers, 1990). Sus características principales son:

• Permite modelar la probabilidad de respuesta correcta como función de:
  • La pertenencia al grupo.
  • El nivel de habilidad.
  • La interacción entre grupo y habilidad.
• Ofrece mayor flexibilidad en el modelado de las relaciones entre las variables.
• Puede incorporar múltiples variables predictoras, como otras características del ítem o del participante.

Procedimiento básico:

1. Se ajustan tres modelos jerárquicos:
   1. Modelo 1: logit(P) = β₀ + β₁θ
   1. Modelo 2: logit(P) = β₀ + β₁θ + β₂G
   1. Modelo 3: logit(P) = β₀ + β₁θ + β₂G + β₃(θ × G)
2. Donde:
   1. P es la probabilidad de respuesta correcta.
   1. θ es el nivel de habilidad.
   1. G es la variable de grupo.
   1. β son los coeficientes de regresión que indican la influencia de las variables.
3. Se comparan los modelos:
   1. Modelo 1 vs Modelo 2: Su propósito es detectar la presencia de DIF uniforme. Si β₂ es significativo, el grupo influye en la probabilidad de éxito.
   1. Modelo 2 vs Modelo 3: Su propósito es evaluar DIF no uniforme. Si β₃ es significativo, hay una interacción entre grupo y habilidad.

Ventajas adicionales:

• La regresión logística es particularmente útil cuando se desea realizar un análisis ítem por ítem, con resultados fácilmente interpretables.
  
  
• Se puede implementar en varios paquetes estadísticos como R, SPSS, SAS o Stata, con funciones específicas para comparar modelos jerárquicos y evaluar ajustes mediante pruebas de verosimilitud o cambios en pseudo R².

Aunque es una buena técnica, su interpretación requiere precaución: la significación estadística no siempre implica un efecto práctico relevante, por ello, se recomienda complementar los análisis con medidas de tamaño del efecto y evaluar su impacto sobre la equidad global del test.

Modelos de Teoría de Respuesta al Ítem (TRI)

La Teoría de Respuesta al Ítem proporciona un marco robusto para la detección del DIF mediante la comparación de las Curvas Características del Ítem (CCI) entre diferentes grupos (De Ayala, 2019). Este enfoque ha ganado prominencia debido a su sofisticación teórica y precisión en la detección, como señalan Tay et al. (2015) en su guía práctica para el análisis de equivalencia de medición. Entre los procedimientos principales en TRI se encuentran la comparación de parámetros y los métodos de área.

En el caso de la comparación de parámetros, descrita por Finch y French (2019), se estiman los parámetros del ítem (a, b, c) para cada grupo y se comparan las diferencias en estos parámetros entre los grupos. Además, se evalúa la significancia estadística de estas diferencias para determinar si existe DIF. Por otro lado, los métodos de área, propuestos por Meade y Wright (2012) consisten en calcular el área entre las CCIs de los grupos, para este procedimiento, se establece un criterio de significancia y se considera la presencia de DIF cuando el área excede un valor crítico.

A partir de lo anterior, la detección del DIF presenta una serie de ventajas y desventajas que deben considerarse dependiendo del contexto de aplicación y los recursos disponibles. Por un lado, los Modelos de Teoría de Respuesta al Ítem, según Tay et al. (2015), destacan por su mayor precisión en la detección del DIF, la separación clara entre la habilidad del sujeto y las propiedades del ítem, la capacidad para detectar DIF no uniforme y la invarianza de los parámetros estimados. Sin embargo, su implementación puede ser desafiante debido a la necesidad de contar con muestras grandes (superiores a 500 por grupo), la complejidad computacional asociada, la necesidad de software especializado.

Análisis Factorial Confirmatorio Multigrupo (AFCM)

El Análisis Factorial Confirmatorio Multigrupo (AFCM) representa una aproximación flexible para la detección del DIF, especialmente útil cuando se trabaja con constructos multidimensionales. Este enfoque ha sido descrito detalladamente por Millsap (2011) en su trabajo sobre invarianza de medición. El procedimiento del AFCM se basa en varios pasos fundamentales, como el establecimiento de invarianza, la evaluación secuencial de modelos y el uso de índices de ajuste.

Cuando evaluamos la invarianza en análisis factorial confirmatorio, seguimos un proceso en tres pasos, primero está la invarianza configural, que simplemente asegura que la estructura factorial sea la misma para los grupos; luego viene la invarianza métrica, que verifica que las cargas factoriales sean equivalentes, es decir, que los ítems se comporten igual en ambos grupos; finalmente, la invarianza escalar, que garantiza que los interceptos también sean iguales, permitiéndonos comparar puntajes directamente entre los grupos, todo esto se evalúa paso a paso, comparando modelos con índices como el CFI, RMSEA y SRMR, además de usar pruebas estadísticas como el chi-cuadrado para confirmar que el ajuste sea adecuado.

Por otro lado, el Análisis Factorial Confirmatorio Multigrupo (AFCM), según Elosua y Wells (2013), permite analizar múltiples grupos simultáneamente y facilita el análisis de constructos multidimensionales, además, proporciona índices de ajuste global que ayudan a evaluar la calidad del modelo y ofrece una gran flexibilidad en la especificación de los modelos. No obstante, el AFCM también enfrenta limitaciones como su sensibilidad al tamaño muestral, la complejidad en la especificación de los modelos, la posibilidad de convergencia inadecuada y la dificultad para manejar ítems dicotómicos, debido a que estos requieren estimadores especiales y violan los supuestos de normalidad del modelo tradicional.

Conclusiones

El Funcionamiento Diferencial de los Ítems (DIF) juega un papel vital en las mediciones psicológicas y educativas, ya que garantiza la equidad en las pruebas, su importancia va más allá de lo estadístico, englobando implicaciones éticas, prácticas y sociales que impactan directamente en los evaluados.

Según estudios actuales, el DIF también puede influir en contextos laborales: afecta pruebas de selección y puede perpetuar desigualdades si no se aborda adecuadamente. Por ejemplo, Fahmi et al. (2023) analizaron el DIF en una escala de equilibrio trabajo‑vida (Work‑Life Balance Scale) entre distintos grupos por género y edad, y encontraron que ciertos ítems presentaban sesgos que podrían distorsionar decisiones si no se corrigen.

Finalmente, identificar el DIF es fundamental para ajustar las herramientas de evaluación a distintas culturas, lenguas y, en general, a características sociodemográficas que puedan influir en el comportamiento estadístico de los ítems. Esto permite asegurar que las pruebas mantengan la misma función en diferentes poblaciones, en un contexto cada vez más globalizado, este proceso es clave para desarrollar instrumentos más inclusivos y con propiedades de validez adecuadas para todos los grupos evaluados.

Herramientas de Software

R y sus Paquetes

1.     difR

•         Funcionalidad: Métodos clásicos y TRI
•         Instalación: install.packages(“difR”)

2.     lordif

•         Especializado en análisis DIF mediante regresión logística ordinal
•         Instalación: install.packages(“lordif”)

SPSS

1.     SPSS DIF-PACK

•         Complemento específico para análisis DIF
•         Incluye procedimientos Mantel-Haenszel y regresión logística
•         Disponible en: IBM SPSS Statistics

Mplus

•         Software especializado en modelamiento de ecuaciones estructurales
•         Capacidades avanzadas para análisis factorial confirmatorio multigrupo
•         Con licencia comercial requerida

Software Gratuito

1.     IRTPRO (versión demo)

•         Análisis DIF basado en TRI
•         Interfaz gráfica intuitiva

2.     jMetrik

•         Software de código abierto
•         Incluye análisis DIF básicos
•         Descarga gratuita en: www.jmetrik.com

Bibliografía

De Ayala, R. J. (2009). The theory and practice of item response theory. Guilford Publications. https://es.scribd.com/document/578193610/The-Theory-and-Practice-of-Item-Response-Theory

Elosua, P., y Wells, C. S. (2013). Detecting DIF in polytomous items using MACS, IRT and ordinal logistic regression. Psychological Assessment, 25(4), 1191-1207. https://files.eric.ed.gov/fulltext/EJ1019157.pdf

Finch, W. H., y French, B. F. (2019). Educational and psychological measurement. Routledge. https://doi.org/10.4324/9781315650951

Fahmi, E., (2023). Analysis of Differential Item Functioning (DIF) on the Work‑Life Balance Scale: Evaluating Bias by Gender and Age. En Proceedings of International Conference, 2023. https://doi.org/10.2991/978-2-38476-032-9_31

Gómez-Benito, J., Hidalgo, M. D., y Guilera, G. (2010). El sesgo de los instrumentos de medición: Tests justos. Papeles del Psicólogo, 31(1). Recuperado de https://www.researchgate.net/publication/41734047_El_sesgo_de_los_instrumentos_de_medicion_Tests_justos

Hidalgo, M. D., y Gómez-Benito, J. (2010). Differential item functioning: Past, present and future. Psicothema, 22(3), 480-487. https://doi.org/10.7334/psicothema2017.183

Holland, P. W., y Thayer, D. T. (1988). Differential item performance and the Mantel-Haenszel procedure. En H. Wainer y H. I. Braun (Eds.), Test validity (pp. 129-145). Lawrence Erlbaum Associates. https://psycnet.apa.org/record/1988-97024-009

Millsap, R. E. (2011). Statistical approaches to measurement invariance. Routledge. https://doi.org/10.4324/9780203821961

Muñiz, J. (2018). Introducción a la Psicometría: Teoría clásica y TRI. Ediciones Pirámide. https://digibuo.uniovi.es/dspace/handle/10651/54694

Swaminathan, H., y Rogers, H. J. (1990). Detecting Differential Item Functioning Using Logistic Regression Procedures. Journal of Educational Measurement, 27, 361-370. https://doi.org/10.1111/j.1745-3984.1990.tb00754.x

Tay, L., Meade, A. W., y Cao, M. (2015). An overview and practical guide to IRT measurement equivalence analysis. Organizational Research Methods, 18(1), 3-46. https://doi.org/10.1177/1094428114553062