Detección y tratamiento de datos faltantes

.

Por: Ana María Fonseca Salgar

.

Los datos faltantes son aquellos que debido a errores en la fase de recolección, ya sean aleatorios o sistemáticos, no se encuentran disponibles a la hora de consolidar un conjunto de datos. Aunque tener valores perdidos es común dentro de las investigaciones, su manejo es de suma importancia, debido a que en caso de tenerlos conlleva a tener una muestra de los datos más pequeña de la esperada y esto puede comprometer la confiabilidad de los resultados de nuestras investigaciones (Kwak y Kim, 2017). 

Teniendo lo anterior en cuenta, es importante saber qué decisiones tomar para tratar con los datos faltantes y qué herramientas pueden ayudarnos en ese proceso. Un primer paso es conocer con qué tipo de datos perdidos nos estamos enfrentando, las categorías más comunes son:

• 1) Completamente al azar (MCAR): Este tipo de dato corresponde a aquellos casos para los cuales se determina que los valores perdidos ocurren de manera completamente aleatoria, es decir, el hecho de que falten valores es independiente de otros valores faltantes o de los valores existentes (Dagnino, 2014). Esto suele ocurrir cuando, por ejemplo, uno de los sujetos de estudio no asiste a todas las sesiones de toma de datos o simplemente a mitad de la aplicación de una encuesta, una persona decide no responder más preguntas (Kwak y Kim, 2017).
• 2) Al azar (MAR): Resulta cuando se determina que la probabilidad de obtener datos faltantes depende solo de los datos observados, pero es independiente de los datos no observados (Dagnino, 2014). Por ejemplo, si en un test sobre salud una de las preguntas habla sobre hábitos alimenticios, es más probable que una persona con sobrepeso no responda este ítem; es decir, los datos faltantes están relacionados a esta variable.
• 3) No al azar (NMAR): Este tipo de dato resulta cuando se determina que los datos faltantes dependen de medidas no observadas, pero es independiente de los datos observados (Dagnino, 2014). Por ejemplo, en una prueba se ha demostrado que el lugar de residencia y el nivel educativo o socioeconómico de los participantes están asociados a los datos faltantes, variables que no eran tenidas en cuenta dentro del estudio (Molina y Galván, 2007).

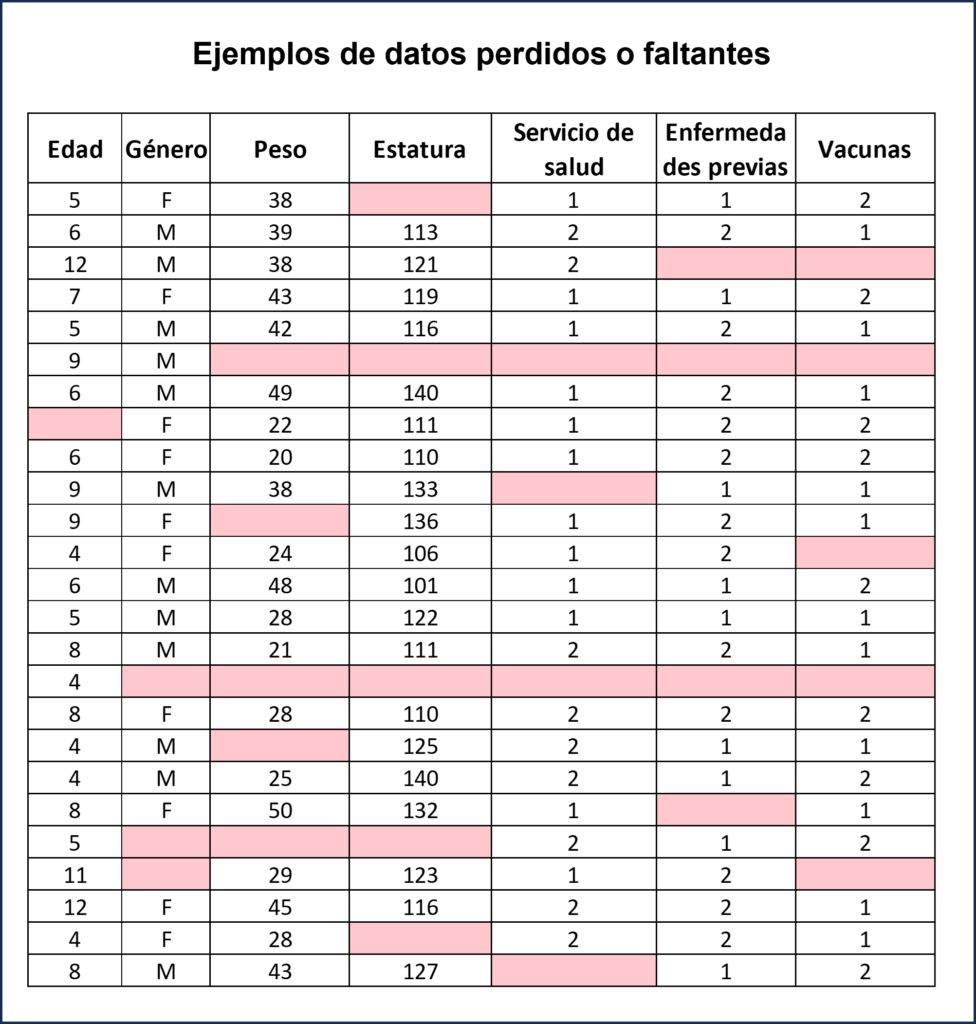
Una vez tengamos claro con qué tipos de datos faltantes estamos trabajando, podemos pasar a escoger algún método para lidiar con ellos. Entre los métodos más utilizados para tratar con estos datos se encuentra el análisis de casos o sujetos completos, el análisis de casos disponibles y la imputación simple. A continuación se explicará un poco sobre qué consiste cada uno de estos.

Análisis de casos o sujetos completos

También llamado “Listwise deletion” en inglés, suele ser el método más utilizado, tanto así que aparece como la opción por defecto en varios programas estadísticos (Van Buuren, 2018). Este método consiste en la eliminación de los datos de los individuos que no brindaron información en alguna de las variables (Carracedo-Martínez y Figueiras, 2006). Entre sus ventajas se encuentra el que brinda cálculos sencillos, y además, si los datos resultan ser del tipo MCAR, entonces las estimaciones de medias, varianzas y regresiones no se ven muy afectados; sin embargo,  si los datos no son de este tipo, la media, índices de correlación y de regresión se pueden ver bastante afectados (Van Buuren, 2018), además de la pérdida de datos que representa.

Análisis de casos disponibles

Conocido como “Pairwise deletion”,  intenta corregir la gran pérdida de datos que puede resultar de usar el método anterior. Este, consiste en incluir todos los datos de las variables observadas, así se tengan datos faltantes en otras variables (Carracedo-Martínez y Figueiras, 2006). Aunque este método resulta bastante útil ya que utiliza toda la información disponible, tiene algunos inconvenientes; como por ejemplo, el que el tamaño de la muestra cambia de variable a variable, lo que puede llegar a complicar los análisis realizados (Carracedo-Martínez y Figueiras, 2006). Así mismo, si los datos faltantes no son del tipo MCAR pueden llegar a verse afectados algunos estadísticos como la media (Van Buuren, 2018).

Imputación

Este método hace referencia a reemplazar los valores faltantes con valores obtenidos por medio de análisis estadísticos realizados con los datos observados (Kwak y Kim, 2017). Esta imputación puede ser simple; por medio de la sustitución por la media no condicional, la imputación cold deck, la imputación hot deck y la imputación por regresión;  o múltiple, por el método Markov Chain Monte Carlo (MCMC), entre otros. A continuación, explicaremos brevemente cada uno de los métodos mencionados.

• 1) Imputación simple:
  • Sustitución por la media no condicional: Tal como lo menciona su nombre, este consiste en reemplazar los valores faltantes con el valor del promedio de los datos totales (Sánchez, 2020). Aunque puede resultar ser la solución más rápida para tratar con los datos faltantes, también puede terminar siendo poco apropiada. Lo anterior, ya que este método asume que los datos faltantes son del tipo MCAR, y ha sido documentado que estadísticos como la varianza pueden resultar siendo subestimados, y del mismo modo, el sesgo y los percentiles se pueden ver afectados (Molina y Galván, 2007; Sánchez, 2020).
  • Imputación Cold Deck: Este método consiste en obtener datos tomados anteriormente (históricos), con características similares a las actuales. Una de sus principales desventajas es que depende de la calidad de los datos tomados anteriormente, además de todos las posibles características intervinientes que pueden resultar diferentes entre un conjunto de datos y otro (Sánchez, 2020; Tema 6: Microdepuración e Imputación de Datos, s. f.). 
  • Imputación Hot Deck: Este método consiste en un procedimiento de duplicación; es decir, se toma un valor ya existente en los datos y se duplica para usarlo así por el dato faltante (Sánchez, 2020). Este procedimiento supone que la distribución de los valores faltantes es la misma que la de los valores observados, lo que hace que el modelo tenga fuertes restricciones (Tema 6: Microdepuración e Imputación de Datos, s. f.).
  • Imputación por regresión: En este método se integra información de otras variables correlacionadas con la variable de interés, para así ajustar un modelo de regresión y predecir el valor de los datos faltantes (Sánchez, 2020; Van Buuren, 2018). Este método puede llegar a presentar estadísticos como la media  sin  sesgo alguno si los datos faltantes son del tipo MCAR; sin embargo, de manera general, los índices de correlación resultan sobreestimados y la variabilidad es subestimada (Van Buuren, 2018).
• Imputación múltiple:
  • Markov Chain Monte Carlo (MCMC): Este método se basa en la simulación de datos mediante cadenas de Markov; la cual se lleva a cabo por medio de la inferencia bayesiana, proceso donde se realizan estimaciones asumiendo que los datos provienen de una distribución normal multivariada. En resumen, se realiza una imputación por cada una de las observaciones usando la matriz de covarianzas, y con los datos obtenidos de este proceso se realizan iteraciones del mismo. Finalmente, se asignan múltiples valores a cada dato faltante para luego combinar los resultados obtenidos (Sánchez, 2020).

Para finalizar, es recomendable que todas las investigaciones realizadas reporten la existencia de datos faltantes, la cantidad de estos, las posibles razones por las que existen estos datos,  y qué método se utilizaron para manejarlos, así como las posibles incidencias de este frente a los resultados del estudio llevado a cabo.

Referencias

Kwak, S. K. & Kim, J. H. (2017). Statistical data preparation: management of missing values and outliers. Korean Journal of Anesthesiology, 70(4), 407. https://doi.org/10.4097/kjae.2017.70.4.407

Dagnino, J. (2014). DATOS FALTANTES (MISSING VALUES). Bioestadística y Epidemiología, 43(4). https://revistachilenadeanestesia.cl/datos-faltantes-missing-values/#:~:text=Alternativas%20para%20mitigar%20los%20datos,predichos%20desde%20los%20datos%20presentes

Grace-Martin, K. (2021, 26 octubre). Confusing Statistical Term #13: MAR and MCAR Missing Data. The Analysis Factor. Recuperado 22 de septiembre de 2022, de https://www.theanalysisfactor.com/mar-and-mcar-missing-data/

Molina, F. & Galván, M. (2007). Imputación de datos: Teoría y práctica. Naciones Unidas. https://repositorio.cepal.org/bitstream/handle/11362/4755/1/S0700590_es.pdfVan Buuren, S. (2018). Flexible Imputation of Missing Data (2nd ed.). Chapman and Hall/CRC. https://doi.org/10.1201/9780429492259