Un mundo sin muestreo

_{Por: José Ignacio García Pinilla}

Un vistazo a este nuevo mundo

Cuando pensamos en un mundo sin muestreo, a simple vista podría parecer que nada ha cambiado, ¡es más!, podría parecer que las cosas han mejorado, una cosa menos en qué pensar cuando estudiamos nuestras clases de bioestadística, estadística social o metodología de la investigación; no más fórmulas para calcular el tamaño adecuado de muestra, no más explicaciones respecto al porqué utilizar una u otra estrategia para escoger nuestros participantes, no más fórmulas para estimar sesgos o intervalos de confianza de nuestras estimaciones sobre la población.

Para lograr mantener los avances logrados en este nuevo mundo, los métodos cualitativos tomarían la batuta sobre la forma de desarrollar el conocimiento en buena parte de las ciencias humanas, a pesar de lo cual otras materias no tendrían tanta suerte para encontrar un reemplazo a sus métodos de investigación y terminarían retornando a la teorización y la especulación. Aunque no sería el fin de los métodos cuantitativos, para avanzar en este frente, nadie podría negarse a participar en una investigación en psicología, sociología o antropología, en medicina todo enfermo debería ubicarse para realizar cualquier afirmación sobre la enfermedad o proceder con cualquier tratamiento, solo información censal y actualizada sería útil para realizar investigaciones educativas y ante la evidente imposibilidad de que todos nos dedicáramos a responder instrumentos sobre toda materia académica de interés, la mayor parte de los avances se reducirían a lo que las investigaciones cualitativas y censales proporcionaran.

Más problemas que soluciones

El breve paso por la fantasía de eliminar parte de la estadística del mundo nos enseña que ignorar el muestreo en la vida de la ciencia moderna traería más problemas que soluciones (y no lo decimos por las potenciales bacanales de algunos científicos cualitativos obviamente), pues en efecto el muestreo es ante todo una solución práctica a un problema concreto, el problema de disponer solo de una parte del universo para conocer con algún grado de certeza la realidad del conjunto completo.

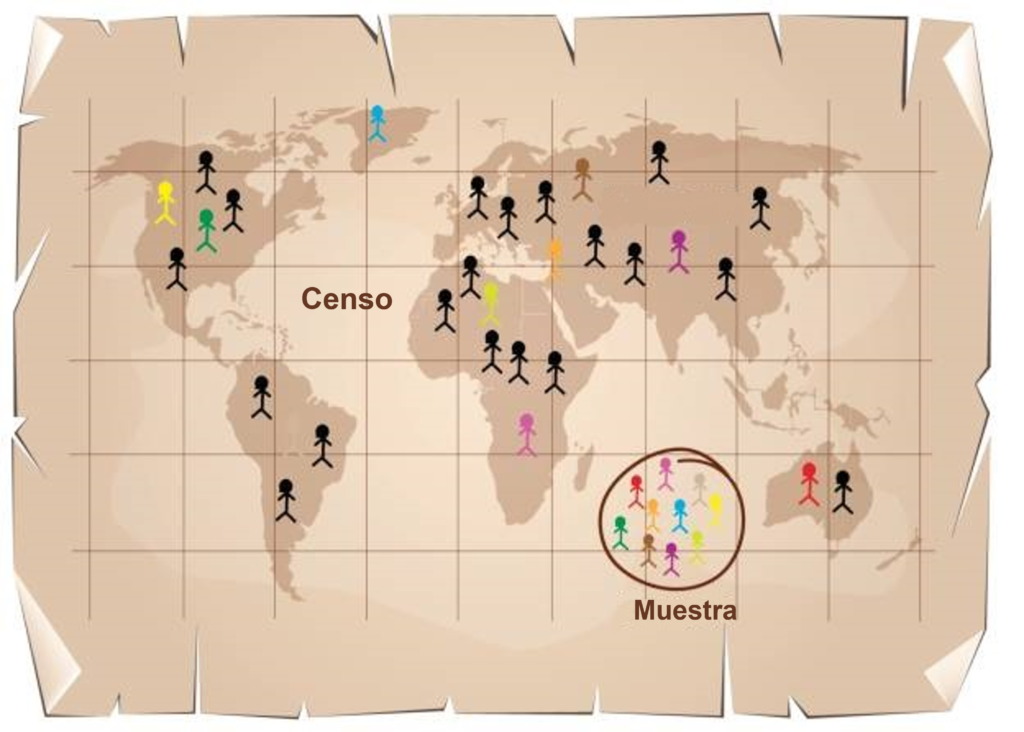
Este problema tan antiguo fue solucionado durante mucho tiempo de dos formas diferentes, realizando costosos censos a las poblaciones de interés (en épocas donde en todo caso hablábamos de menos del 10% de la población actual y donde generalmente poco importaba contabilizar a la mayor parte de la población, como mujeres, niños, siervos, esclavos, vagabundos, lisiados, etc.) o ignorando deliberadamente los fenómenos para los cuales era imposible tener datos sobre toda la población. Sin embargo, con la consolidación de los Estados modernos, la estadística tuvo un especial impulso como herramienta para el control fiscal y el conocimiento de los dirigentes políticos sobre las necesidades de sus gobernados con el fin de tomar decisiones que ayudaran a crear mejores condiciones para la población, especialmente en el caso de las sociedades democráticas o las de absolutismo ilustrado.

En este contexto, como suele ser la regla, los recursos escaseaban, además la población crecía a pasos agigantados, de manera que las aspiraciones de obtener información censal sobre cada nueva cuestión de interés, incluida la educación, se marchitaban rápidamente. Es aquí donde nace la teoría muestral y donde la estadística inferencial se abre paso, ya que según sus postulados era posible conocer características de una población realizando cuidadosamente observaciones solo sobre una parte. El cuidado de la observación no solo consistía en disminuir el error en la medición, aspecto propio de los instrumentos utilizados, sino también del modo en cómo se seleccionaban dichas observaciones, objeto de la teoría muestral.

Claramente, la solución al problema de la escasez de observaciones no llegó de la noche a la mañana, pues los trabajos de diversas personalidades fueron cruciales para su cimentación adecuada, siendo obligatorio nombrar figuras como Abraham de Moivre (1667-1754) con la propuesta de la curva normal, Pierre-Simon Laplace (1749-1827) con la identificación de la distribución de los errores en observaciones, Carl Friedrich Gauss (1777-1855) con la identificación de la recta de regresión para describir la relación entre dos variables, Adolphe Quetelet (1796-1874) con la constatación de que características humanas como la masa corporal siguen una curva normal, Francis Galton (1822-1911) con la concepción de la correlación, Karl Pearson (1857-1936) con la matematización de la correlación (r), la distribución y la prueba Ji cuadrado, las tablas de contingencia, los histogramas y la curtosis, así como Arthur Bowley (1869-1957) con la utilización de técnicas de muestreo para las investigaciones sociales y econométricas.

Algunos conceptos fundamentales

Aun con lo dicho hasta este punto, quizá no sean claros algunos de los conceptos que tuvieron que afinarse para que la inferencia estadística tuviera sentido, siendo el muestreo una de las herramientas para lograrlo. Para clarificarlos nos valdremos de un ejemplo sencillo pero familiar, juzgar la calidad de la clase de un docente universitario, teniendo en cuenta el hecho de que en la cotidianidad los seres humanos hacemos constantes muestreos para conocer el mundo que nos rodea (aun cuando en muchos casos sean observaciones claramente sesgadas para un observador externo).

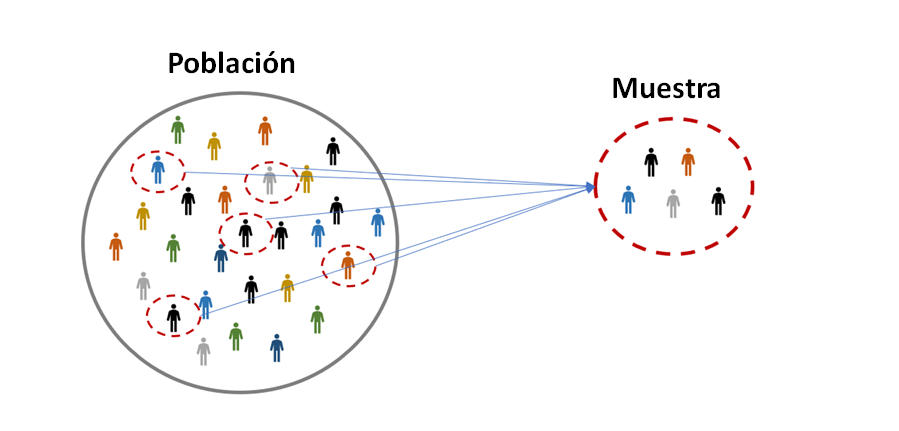
Para nuestro ejemplo vamos a suponer que en la universidad a la que asistimos disponemos de tres profesores que dictan un curso que es de nuestro interés, digamos Psicología Educativa, y casualmente tenemos la posibilidad de conocer una parte de las clases de cada uno de los profesores antes de decidir con cuál de ellos finalmente inscribir el curso el siguiente semestre. Tenemos ante nosotros una de las primeras cuestiones que debemos comprender con claridad, la diferencia entre población o universo y muestra. En nuestro ejemplo el universo de observaciones son todas las clases que dictará cada uno de los profesores, pero cuidado, estamos hablando de tres universos diferentes, porque las inferencias que realicemos sobre un profesor solo serán aplicables a las clases de ese profesor, no a las de los otros dos, al menos en principio, por lo que cada profesor funge como el creador de un universo de clases, de las cuales nosotros seleccionaremos algunas para asistir y tomar nuestra decisión, esta selección de clases es lo que llamamos muestra, y tal como ocurre con los universos, hablamos aquí de tres muestras diferentes.

Siguiendo con nuestro ejemplo, podríamos calificar cada clase según una escala subjetiva de 1 a 10, donde 1 sería “¡la peor clase a la que he asistido en mi vida!” y 10 sería “¡la mejor clase a la que he podido asistir en mi breve existencia!”, de tal forma que juntemos en una sola calificación todos los detalles que nos interese tener en cuenta para decir que una clase es de calidad, como la actitud hacia los estudiantes, la didáctica, la profundidad en las explicaciones o lo dinámico de las presentaciones, entre otras. Tendríamos que recordar que es posible que algunas clases sean mejores que otras, ya que hablamos de humanos, no de robots, por lo que nuestras calificaciones sobre la clase podrían cambiar cada vez que fuéramos a una nueva sesión. Aquí tenemos a mano otro concepto clave, el de variabilidad aleatoria, el cual nos indica que una variable, por ejemplo nuestra evaluación sobre la calidad de la clase, puede tomar cualquier valor dentro de una escala de medición preestablecida, como nuestra escala de 1 a 10, siempre y cuando no tengamos certeza del valor que va a tener esa variable al final de nuestra observación, en otras palabras, no sabríamos de antemano cual es la calidad de la clase a la que estamos por entrar.

Volviendo a las clases, podríamos empezar con el profesor P, el cual dictará un máximo de 16 clases en todo el curso que dura un semestre, ¡pero momento!, no asistiremos a todas las clases, en cambio iremos a 4, que parece un buen número para juzgar a alguien, y a cada clase la calificaremos según nuestra escala subjetiva. Si pensamos por un momento en todas las posibles clases que este profesor puede hacer, intentando competir con el Doctor Strange, es sensato pensar que la mayoría serían muy “normales”, clases que se disfrutan pero no te cambian la vida, mientras que habría un grupo cada vez más pequeño de clases tanto muy malas, como para perder todo interés en el tema, como de clases muy buenas, como para dedicar tu vida entera al estudio de esas cuestiones.

Es aquí donde sale a escena el concepto de distribución, el cual se basa en el hecho de que dado un intervalo de posibles valores para una variable, como nuestra escala subjetiva para la calidad de la clase del profesor, es previsible que, si se repite la observación muchas veces, podremos observar que algunos resultados tienden a ser más frecuentes que otros si no estamos hablando de un fenómeno completamente aleatorio, lo cual se traduce en que de hecho en muchos fenómenos de la naturaleza, mas no en todos, los valores intermedios suelen ser los más frecuentes, mientras que los valores más extremos suelen ser poco frecuentes. En otras palabras, si esto es cierto para las calificaciones que haremos de las clases, será más probable que nos encontremos con una clase intermedia del profesor a que nos encontremos con una muy buena o muy mala, mas no imposible.

Rastrillando la superficie

Este breve repaso por la idea del muestreo no es más que la superficie de la mina de soluciones que puede ofrecernos la teoría muestral, pocas comparadas con las que contiene el monte de la estadística inferencial, incluso aquellas que aún no hemos descubierto. Las vetas que hemos ido descubriendo están listas para ser exploradas con mayor atención, pues al entrar en el detalle de cada una de ellas podremos encontrar respuestas a problemas recurrentes en la construcción y verificación del conocimiento, pero más especialmente, podremos encontrar herramientas de juicio que nos permitan evaluar críticamente afirmaciones sobre nuestros campos profesionales que cotidianamente enfrentamos, basadas muchas veces en investigaciones, encuestas o sondeos de dudosa calidad.