Que es la Colinealidad y Multicolinealidad y como saber si nuestras variables son colineales o multicolineales entre sí.

.

Por: Uriel Alejandro Arevalo Rochel

Normalmente en estadística, se utilizan variables dependientes y variables independientes. Uno de los objetivos de trabajar con una o más variables independientes, es llegar a un modelo predictor por medio de la regresión lineal (simple o múltiple) y así poder determinar cómo se comportará una variable dependiente. Teniendo en cuenta lo anterior, y sabiendo que en ciencias humanas es muy probable trabajar con más de una variable independiente, nos surge un tema algo difícil de tratar ¿Qué pasaría si una de nuestras variables independientes es una combinación lineal de otra de nuestras variables independientes, o de muchas de nuestras variables dependientes?

 Antes de asustarse, permítame explicarle brevemente cómo funcionan las combinaciones lineales. Suponga que usted tiene un conjunto de variables independientes K, M, L y P, estas variables deberían ser independientes entre sí para poder trabajar con ellas, pero si por azares del destino una de sus variables es una combinación de otras (por ejemplo, K) dicha variable sería explicada por las demás variables combinadas, en este caso concreto: K= 1* M+2*L+3*P donde 1, 2 y 3 son constantes. Si al tratar sus datos alguna de sus variables independientes o predictoras tienen este comportamiento, sus variables son colineales o multicolineales y ahora sí es momento de asustarse. 

La colinealidad entonces nos habla de la dependencia o correlación entre sus variables, es decir, una de sus variables puede estar siendo explicada o ser combinación lineal de una o de varias de sus variables, y esta situación es problemática en estadística ya que la colinealidad o multicolinealidad lleva a cuestas ciertos problemas que nos impiden realizar una regresión lineal y llegar a un modelo predictor.

Problemas de la colinealidad y multicolinealidad.

Al tener variables colineales o multicolineales, suelen aparecer problemas en la regresión lineal, ya que una de las variables independientes explica en gran medida o en su totalidad otra de nuestras variables, esto hace que nuestro modelo predictor falle y no podamos definir con exactitud la variable dependiente. Otro de los problemas de la colinealidad (y que va de la mano con el primer problema presentado) es que reduce la significancia estadística de nuestros resultados llevándonos a datos erróneos. También puede llegar a hacer nuestro modelo de regresión lineal insoluble, ya que, al hacer nuestra matriz, la colinealidad hace que el determinante de esta sea cero o esté muy cerca a cero, dejándonos sin una matriz prima para poder invertir la matriz original, o dándonos valores imprecisos al invertir la matriz causadas por un determinante muy cercano a cero. 

¿Cómo comprobar si nuestras variables son colineales o multicolineales? 

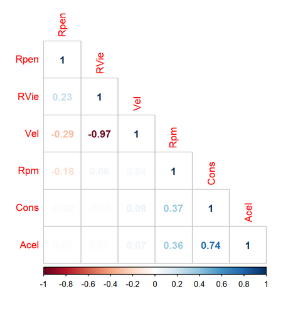
Lo primero que podemos hacer para comprobar si nuestras variables tienen correlaciones entre sí, es evaluar nuestras variables en una matriz de correlación, en esta matriz, podemos comparar la correlación de cada una de nuestras variables por medio de un programa estadístico que nos arroja un número r de correlación o coeficiente de correlación (esto teniendo en cuenta que nuestros datos sean datos paramétricos), a continuación se mostrará un ejemplo tomado de la página web https://rpubs.com/adrianRm/multicolinealidad .

Como podemos observar en la matriz de correlación, cuatro de las variables expuestas en la matriz guardan una correlación significativa, ya que las variables VEL y RVIE tienen r muy cercano a 1 y las variables CONS y ACEL tienen un r que se acerca peligrosamente a 1

Para ilustrar de una mejor manera este problema de colinealidad, mostraremos un gráfico sacado del mismo ejercicio expuesto en la página https://rpubs.com/adrianRm/multicolinealidad .

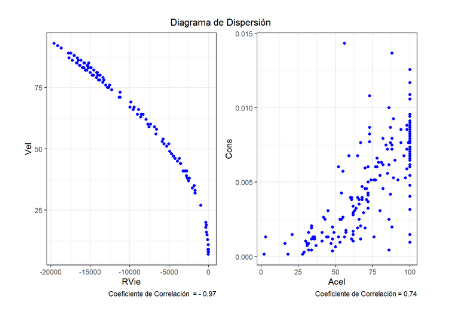
Vemos entonces cómo las variables VEL y RVIE se comportan al graficarla una contra la otra, lo que nos llega a pensar que una de las dos variables nos está dando datos predictores irrelevantes o que una de las dos explique a la otra y nos lleve a los problemas que nos genera tener variables colineales. 

Una vez entonces tenemos nuestra matriz de correlaciones, debemos estar atentos a valores que sobrepasen  r≥0.9 ya que con valores tan cercanos a 1 nuestras variables pueden estar correlacionadas entre sí. Tenga en cuenta que valores muy cercanos a 1 indican una correlación casi perfecta para sus variables, pero esto también acarrea la posibilidad de que entre sus variables independientes sean colineales.

Podemos también utilizar otros conceptos como el de tolerancia o el factor de la inflación de la varianza (FIV) para determinar si nuestras variables son colinealmente fuertes o débiles: 

• Tolerancia: si elevamos r al cuadrado y utilizamos T=1-r2 donde T es la tolerancia, vemos que valores muy cercanos a 0.1 indican que hay un índice alto de colinealidad.
• Factor de la inflación de la varianza (FIV): utilizando FIV=1T  Los valores que sobrepasen a 10, pueden considerarse de colinealidad fuerte.

Bibliografía. 

Casal, R., Costa, J., Oviedo, M. (2021). El problema de la colinealidad. https://rubenfcasal.github.io/aprendizaje_estadistico/colinealidad.html

Ciencias sin sesos. (28 de febrero de 2017). Colinealidad en regresión lineal múltiple. https://www.cienciasinseso.com/colinealidad-en-regresion-lineal-multiple/

Godínez, J., Ramírez-Valverde, G., Reyes-Carreto, R., Ariza-Hernandez, J., & Barrera-Rodriguez, E. (2012). La colinealidad y la separación en los datos en el modelo de regresión logística. Agrociencia, 46(4), 411-425. Recuperado en 08 de marzo de 2023, de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1405-31952012000400008&lng=es&tlng=es.

HRC. (f.s). El problema de la colinealidad. http://www.hrc.es/bioest/Reglin_15.html

IBM. (13 de septiembre de 2022). Regresión lineal: Estadísticos. https://www.ibm.com/docs/es/spss-statistics/saas?topic=regression-linear-statistics

Keepcoding. (12 de diciembre de 2022). ¿Qué es la colinealidad y como corregirla? https://keepcoding.io/blog/que-es-la-colinealidad-y-como-corregirla/

López, E. (1998). Tratamiento de la colinealidad en regresión múltiple. Psicothema. https://www.psicothema.com/pi?pii=181

Martinez, A. (2 de septiembre de 2020). Análisis de multicolinealidad. Rpubs. https://rpubs.com/adrianRm/multicolinealidad