¿Qué es la curva característica del ítem – CCI – en IRT?  

.

Por: Cristian Stiven Tarapues

¿Sabías que solo el 30% de los tests utilizados en educación y psicología tienen características psicométricas adecuadas? (Smith, 2022). Esta impactante estadística destaca la importancia de implementar teorías de medición como la Teoría de Respuesta al Ítem (IRT) para desarrollar evaluaciones precisas y confiables (Hambleton y Swaminathan, 2010). Ya que es una teoría que permite estimar con mayor precisión las habilidades o rasgos latentes que se están midiendo en un instrumento de medición.

La IRT modela la dificultad de los ítems y la habilidad de los examinados (De Ayala, 2009). Sus conceptos clave son la Curva Característica del Ítem (CCI) y la Curva Característica del Test (CCT) (Baker, 2001). La CCI representa las propiedades psicométricas de cada ítem individual, como dificultad y, en modelos de más parametros, discriminación y la adivinanza. La CCT muestra la relación entre el nivel de habilidad y las probabilidades de responder correctamente a cada uno de los ítems o elementos que componen el test (Hambleton et al., 1991).

En este blog, explicaremos la CCI en IRT. Descubriremos cómo analizar los ítems de forma individual, para mejorar la calidad psicométrica de los instrumentos (Fan, 1998). ¡Comencemos!

¿Qué es la CCI?

La Curva Característica del Ítem (CCI) es la representación de una función matemática que describe la relación entre la habilidad del examinado (θ) y la probabilidad de responder correctamente a un ítem en particular (P(θ)).

Además, proporciona información valiosa sobre las propiedades psicométricas de un ítem, como su dificultad, capacidad de discriminación y adivinación. Dependiendo del modelo TRI utilizado, la CCI puede tener diferentes formas y parámetros (Bond & Fox, 2015).

Para el modelo IRT de un parámetro (1PL), la fórmula del CCI es:

En el Modelo Rasch (1PL), se asume que todos los ítems tienen el mismo parámetro de discriminación (ai = 1), por lo que solo se estima el parámetro de dificultad bi (Wright & Stone, 1979). Esto hace que el CCI dependa únicamente de la diferencia entre la habilidad del examinado y la dificultad del ítem.

Una característica distintiva del Modelo Rasch es que las curvas características de los ítems son paralelas entre sí. Esto se debe a que el modelo asume una discriminación constante (pendiente) para todos los ítems, típicamente fijada en 1. Al no estimar la discriminación de manera individual para cada ítem, todas las curvas tienen la misma pendiente, resultando en curvas paralelas. Este paralelismo facilita la comparación e interpretación de los parámetros de dificultad bi (Bond & Fox, 2015). Como resultado, se obtiene una escala de medición lineal y unidimensional de la habilidad latente.

En cuanto a la interpretación:

• Si la habilidad del examinado (𝜃𝑗) es igual a la dificultad del ítem (𝑏𝑖), la probabilidad de que el examinando responda correctamente al ítem es 0.5.
• Si la habilidad del examinado es mayor que la dificultad del ítem, la probabilidad de una respuesta correcta es mayor que 0.5.
• Si la habilidad del examinado es menor que la dificultad del ítem, la probabilidad de una respuesta correcta es menor que 0.5.

Para el modelo de dos parámetros (2PL), la fórmula es:

Específicamente, el parámetro ai indica cuán efectivo es un ítem para distinguir entre examinados de diferente habilidad. Un valor alto de ai implica que el ítem puede discriminar bien, mientras que un valor bajo sugiere que el ítem no es tan sensible a las diferencias en habilidad (Hambleton et al., 1991).

Por otro lado, bi señala la posición a lo largo del continuum de habilidad donde la probabilidad de respuesta correcta es 50%. Determinando así la dificultad del ítem; un valor alto de biindica un ítem más difícil, y un valor bajo indica un ítem más fácil. Estos parámetros combinados permiten una evaluación precisa y justa, ajustando la probabilidad de respuesta correcta según la habilidad del examinado y las características del ítem.

Algunos modelos IRT de tres parámetros incluyen además un parámetro de pseudo-azar o adivinación (3PL), quedando la fórmula:

En estos modelos de tres parámetros, el parámetro 𝑐𝑖 representa la probabilidad de que un examinado de muy baja habilidad responda correctamente al ítem por azar (Embretson & Reise, 2000). Esto es especialmente relevante para ítems de opción múltiple con un número limitado de alternativas. Este parámetro captura la posibilidad de que un examinando adivine la respuesta correcta, proporcionando una evaluación más precisa de la habilidad real del examinado.

Al incorporar 𝑐𝑖 el modelo 3PL puede diferenciar mejor entre las respuestas correctas obtenidas por conocimiento y aquellas obtenidas por adivinación, mejorando la validez de la evaluación y ofreciendo una representación más detallada del comportamiento del ítem en el test.

Aplicaciones de la CCI

La Curva Característica del Ítem (CCI) es una herramienta fundamental en la Teoría de Respuesta al Ítem (IRT) que ofrece información detallada sobre el funcionamiento de cada ítem individual en un test. Sus aplicaciones son diversas y de gran importancia en el campo de la psicometría:

• Selección y refinamiento de ítems: La CCI permite identificar ítems con propiedades psicométricas óptimas, facilitando la selección de los más adecuados para un test. Esto mejora la calidad general del instrumento de medición (Embretson & Reise, 2000).
• Análisis del funcionamiento diferencial de los ítems (DIF): La comparación de CCIs entre diferentes grupos demográficos ayuda a detectar posibles sesgos en los ítems, contribuyendo a la equidad en la evaluación (Camilli & Shepard, 1994).
• Calibración de ítems: La CCI es fundamental en el proceso de calibración de ítems, especialmente en la creación de bancos de ítems para tests adaptativos computarizados (van der Linden & Glas, 2000).
• Evaluación de la precisión de medición: A través de la función de información del ítem, derivada de la CCI, se puede determinar la precisión de medición de cada ítem en diferentes niveles de habilidad (Baker, 2001).
• Desarrollo de nuevos modelos de IRT: El estudio de las CCIs ha llevado al desarrollo de modelos IRT más sofisticados, como los modelos multidimensionales y los modelos de respuesta nominal (Reckase, 2009).
• Vinculación y equiparación de tests: Las CCIs son utilizadas en procesos de vinculación y equiparación de diferentes formas de un test, asegurando la comparabilidad de las puntuaciones (Kolen & Brennan, 2014).
• Diagnóstico de problemas en ítems:El análisis de la forma de la CCI puede revelar problemas en la redacción o estructura de los ítems, guiando su revisión y mejora (Haladyna & Rodriguez, 2013).
• Optimización de tests de clasificación:En contextos donde se requiere clasificar a los examinados en categorías (por ejemplo, aprobado/reprobado), las CCIs ayudan a seleccionar ítems que maximizan la precisión en los puntos de corte relevantes (Hambleton et al., 1991).

Estas aplicaciones demuestran la versatilidad y el valor de la CCI en el desarrollo, evaluación y mejora de instrumentos psicométricos, contribuyendo significativamente a la precisión y equidad en la medición psicológica y educativa.

Propiedades e Interpretación de la CCI

Las propiedades e interpretación de las CCI son cruciales para comprender el funcionamiento de los ítems y tomar decisiones informadas en el desarrollo y análisis de test.

Propiedades de la CCI

• Forma de la curva: La forma del CCI está determinada por los parámetros del modelo IRT utilizado, como la dificultad, la discriminación y, en algunos casos, la pseudoadivinación (Embretson & Reise, 2000).
• Rango de valores: La curva del CCI se encuentra entre 0 y 1 en el eje vertical (y), representando las probabilidades de respuesta correcta. En el eje horizontal (x), la escala típicamente representa la habilidad o rasgo latente del examinado, generalmente expresada en unidades de desviación estándar, con valores que suelen oscilar entre -3 y +3 (De Ayala, 2009).
• Simetría: En los modelos IRT dicotómicos, el CCI suele tener una forma simétrica y en forma de “S” (Hambleton & Swaminathan, 2010).
• Pendiente: La pendiente de la curva del CCI indica el poder de discriminación del ítem. Una pendiente más empinada implica una mayor capacidad para diferenciar entre examinados de diferentes niveles de habilidad (Baker, 2001).

En la gráfica, se pueden observar y analizar tres parámetros clave en el contexto del modelo IRT (Teoría de Respuesta al Ítem) de tres parámetros: dificultad, discriminación y pseudoadivinación. A continuación, se explican cada uno de estos parámetros en detalle:

• Parámetro de dificultad: La dificultad del ítem se representa en el eje horizontal de la gráfica, que corresponde a la habilidad del examinando. Específicamente, el parámetro de dificultad se localiza en el punto donde la CCI cruza el valor de 0.5 en el eje vertical de probabilidad. Este es el nivel de habilidad en el cual un examinando tiene un 50% de probabilidad de responder correctamente al ítem. En la gráfica, este punto indica el umbral de habilidad necesario para que el ítem sea considerado “medio” en términos de dificultad.
• Parámetro de discriminación: La discriminación del ítem está representada por la pendiente de la CCI en su punto de inflexión, que es el área de la curva donde la probabilidad de acierto cambia más rápidamente. Una pendiente más pronunciada en este punto sugiere que el ítem es más efectivo para diferenciar entre examinados cuyas habilidades están alrededor del nivel de dificultad del ítem.
• Parámetro de pseudoadivinación: El parámetro de pseudoadivinación se observa en la intersección de la CCI con el eje vertical en el extremo izquierdo de la gráfica (cuando la habilidad es muy baja). Este parámetro indica la probabilidad mínima de que un examinando con habilidad muy baja (incluso negativa) responda correctamente al ítem por azar. En la gráfica, este valor se refleja en la altura donde la curva comienza, mostrando que, incluso con habilidades muy bajas, existe una cierta probabilidad de acierto debido al azar.

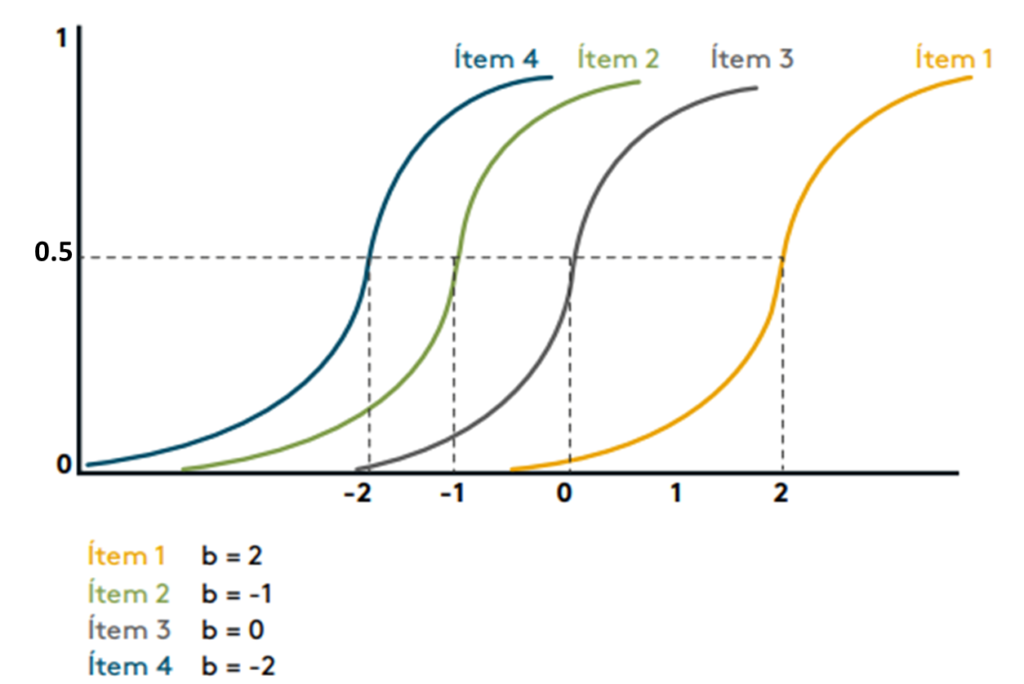
En la gráfica, se observan cuatro ítems, cada uno con un parámetro de dificultad diferente (denotado por la letra 𝑏). El parámetro 𝑏 indica el punto en el que la probabilidad de responder correctamente es del 50% (0.5). Así, los ítems con 𝑏 más alto son más difíciles, ya que requieren un mayor nivel de habilidad para alcanzar esa probabilidad del 50%.

• Ítem 1 (amarillo, 𝑏=2): Es el más difícil, ya que la probabilidad de respuesta correcta es del 50% solo cuando la habilidad es 2.
• Ítem 2 (verde, 𝑏=−1): Es más fácil, con un 𝑏 negativo, la probabilidad del 50% se alcanza con una habilidad de -1.
• Ítem 3 (gris, 𝑏=0): Es de dificultad media, ya que la probabilidad del 50% se da cuando la habilidad es 0.
• Ítem 4 (azul, 𝑏=−2): Es el ítem más fácil, ya que solo se necesita un nivel de habilidad de -2 para tener una probabilidad del 50% de responder correctamente.

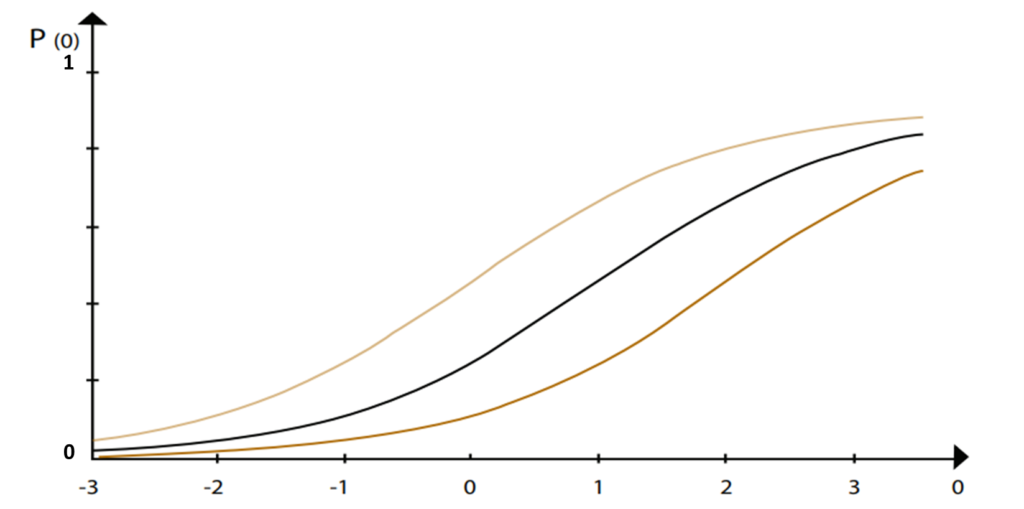
En la gráfica se observan tres Curvas Características del Ítem (CCI) que muestran la probabilidad de respuesta correcta en función del nivel de habilidad de los examinandos, denotado en el eje horizontal. Aunque todas las curvas tienen el mismo nivel de discriminación (es decir, todas son igualmente efectivas para diferenciar entre individuos con diferentes niveles de habilidad), difieren en cuanto a su dificultad.

• Curva superior (beige): Representa un ítem fácil. La probabilidad de que un examinando con baja habilidad responda correctamente es relativamente alta, y esta probabilidad se aproxima a 1 a medida que la habilidad aumenta. Esto significa que incluso individuos con poca habilidad tienen buenas posibilidades de acertar este ítem.
• Curva del medio (negro): Corresponde a un ítem de dificultad media. En este caso, la probabilidad de respuesta correcta es baja para individuos con baja habilidad, alrededor de 0,5 para individuos con habilidad promedio, y se acerca a 1 solo para los examinandos con un nivel de habilidad más alto.
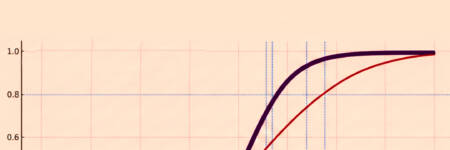
• Curva inferior (marrón): Representa un ítem difícil. La probabilidad de que un examinando responda correctamente es baja en casi toda la escala de habilidad, aumentando sólo cuando se alcanzan los niveles más altos de habilidad. Incluso en estos niveles, la probabilidad máxima de acierto no alcanza 1, siendo alrededor de 0,8 en el punto más alto de la habilidad mostrada (+3).

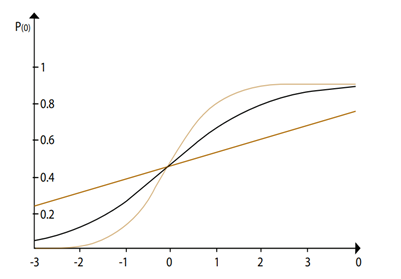
En la gráfica se ilustran tres Curvas Características del Ítem (CCI) que muestran cómo varía la probabilidad de respuesta correcta en función del nivel de habilidad, pero con énfasis en la discriminación de los ítems. Aunque todas las curvas tienen el mismo nivel de dificultad, es decir, están centradas en la misma posición a lo largo del eje horizontal, difieren en su capacidad para discriminar entre individuos con diferentes niveles de habilidad.

• Curva superior (beige): Representa un ítem con un alto nivel de discriminación. Esto significa que la pendiente de la curva en la parte central es muy pronunciada. Una pequeña variación en la habilidad de los examinandos produce un cambio dramático en la probabilidad de responder correctamente. Por ejemplo, para niveles de habilidad ligeramente menores al punto central, la probabilidad de acierto es mucho menor que 0,5, mientras que, para niveles ligeramente superiores, la probabilidad se acerca rápidamente a 1. Este tipo de ítem es muy efectivo para diferenciar entre individuos que tienen habilidades cercanas a la dificultad del ítem.
• Curva del medio (negra): Corresponde a un ítem con un nivel de discriminación moderado. La pendiente en la parte central de la curva es menos pronunciada que en la curva superior. La probabilidad de respuesta correcta cambia de manera más gradual a medida que aumenta la habilidad. Sin embargo, aún se observa una clara diferencia en la probabilidad de acierto entre individuos con habilidades bajas (probabilidad cercana a 0) y aquellos con habilidades altas (probabilidad cercana a 1).
• Curva inferior (marrón): Representa un ítem con poca discriminación. La pendiente de esta curva es muy suave, lo que indica que la probabilidad de respuesta correcta cambia lentamente a lo largo del rango de habilidades. Incluso en niveles bajos de habilidad, la probabilidad de acierto es razonablemente alta, y apenas aumenta cuando se alcanzan altos niveles de habilidad. Esto sugiere que este ítem no es muy efectivo para distinguir entre individuos con diferentes niveles de habilidad.

Supuestos de los modelos IRT y sus implicaciones en el CCI

Los modelos de la Teoría de Respuesta al Ítem (IRT) se basan en varios supuestos fundamentales que tienen implicaciones directas en la forma e interpretación de la Curva Característica del Ítem (CCI). Entre estos supuestos se encuentran la unidimensionalidad, la independencia local y la invarianza de los parámetros de los ítems, la violación de los supuestos de los modelos IRT puede distorsionar la forma del CCI de diversas maneras. Por ejemplo, puede hacer que las curvas sean más planas o más empinadas de lo esperado, o que se desplacen horizontalmente (cambios en la dificultad) o verticalmente (cambios en la discriminación) (Hambleton & Swaminathan, 2010).

Estas distorsiones pueden llevar a interpretaciones erróneas de los parámetros de los ítems y a una representación inexacta de la relación entre la habilidad y la probabilidad de respuesta correcta. Por lo tanto, es crucial evaluar cuidadosamente el cumplimiento de los supuestos antes de utilizar e interpretar los CCI en la práctica.

Unidimensionalidad: Los modelos de Teoría de Respuesta al Ítem (IRT) asumen que existe una sola habilidad o rasgo latente (dimensión) que influye en las respuestas de los examinados a los ítems. Este supuesto es crucial porque si un ítem evalúa más de una habilidad, la relación entre la habilidad latente y la probabilidad de respuesta correcta podría distorsionarse, afectando tanto la forma de la Curva Característica del Ítem (CCI) como la interpretación de los resultados.

Por ejemplo, supongamos que un ítem está diseñado para evaluar habilidades de cálculo algebraico. Si, además, el ítem requiere conocimientos de geometría para ser respondido correctamente, entonces no se estaría midiendo exclusivamente la habilidad en álgebra. Esto violaría el supuesto de unidimensionalidad porque estaríamos involucrando múltiples dimensiones (álgebra y geometría), lo que podría llevar a estimaciones sesgadas de los parámetros del ítem, como la dificultad y la discriminación.

Cuando se viola el supuesto de unidimensionalidad, las CCIs pueden no representar adecuadamente la relación entre la habilidad y la probabilidad de respuesta correcta. Esto no solo afecta la interpretación de las CCIs, sino que también compromete la validez del uso de los modelos IRT en la evaluación de los examinados, conduciendo a inferencias erróneas sobre la habilidad de los mismos y sobre las propiedades de los ítems evaluados (Hambleton et al., 1991).

Independencia local: Este supuesto establece que, para un nivel dado de habilidad, las respuestas de un examinado a los ítems son estadísticamente independientes. Si se viola este supuesto, es decir, si las respuestas a los ítems están relacionadas más allá del efecto de la habilidad latente, la forma del CCI puede distorsionarse (Embretson & Reise, 2000).

La dependencia local puede ocurrir, por ejemplo, cuando los ítems comparten contenido o claves similares, o cuando los examinados utilizan estrategias de respuesta específicas. Esto puede resultar en una sobreestimación o subestimación de los parámetros del ítem y, en consecuencia, una representación inexacta del CCI.

Invarianza de los parámetros de los ítems: Los modelos IRT asumen que los parámetros de los ítems (dificultad, discriminación, pseudoadivinación) no varían entre diferentes grupos de examinados con la misma habilidad latente. Si este supuesto se viola, es decir, si los parámetros de los ítems difieren entre grupos (funcionamiento diferencial del ítem), la forma del CCI puede ser diferente para cada grupo (De Ayala, 2009).

Esta falta de invarianza puede deberse a sesgos culturales, lingüísticos o de otro tipo en los ítems. Ignorar esta violación del supuesto puede llevar a estimaciones sesgadas de los parámetros de los ítems y a comparaciones injustas entre los grupos.

Evaluación del ajuste del CCI al modelo IRT

Según Hambleton y Swaminathan (2010), la evaluación del ajuste de la CCI al modelo IRT es un paso crucial en el análisis psicométrico. Esta evaluación permite determinar si la relación entre la habilidad del examinado y la probabilidad de responder correctamente un ítem se ajusta adecuadamente a las predicciones del modelo IRT utilizado. Un mal ajuste puede indicar violaciones de los supuestos del modelo o problemas con los ítems, lo que compromete la validez e interpretabilidad de las mediciones derivadas del test.

Existen varios estadísticos que permiten evaluar el grado de ajuste entre los datos observados y las predicciones del modelo IRT, incluyendo la CCI. Uno de los más utilizados es la prueba de chi-cuadrado (Hambleton & Swaminathan, 2010). Esta prueba compara las frecuencias observadas y esperadas de respuestas correctas e incorrectas para cada ítem, en diferentes niveles de habilidad. Valores altos del estadístico chi-cuadrado indican un desajuste significativo entre los datos y el modelo, sugiriendo que el CCI puede no representar adecuadamente la relación entre la habilidad y la probabilidad de respuesta correcta.

Otros estadísticos de ajuste comunes son los residuos estandarizados y las estadísticas de likelihood, que también comparan los datos observados con los valores predichos por el modelo IRT.

Además de los estadísticos numéricos, los gráficos de diagnóstico son herramientas para evaluar visualmente el ajuste del CCI al modelo IRT (De Ayala, 2009). Uno de los gráficos más utilizados es la curva característica observada frente a la curva característica esperada. Si el CCI se ajusta bien al modelo, las curvas observada y esperada deberían ser esencialmente similares. Por el contrario, desviaciones sustanciales entre estas curvas indicarían un mal ajuste de la CCI, lo que podría reflejar violaciones de los supuestos del modelo o problemas con el ítem en cuestión. Otros gráficos útiles incluyen los gráficos de residuos y los diagramas de dispersión de las puntuaciones observadas versus las esperadas.

En resumen, un mal ajuste de la CCI puede afectar las inferencias realizadas sobre los niveles de habilidad de los examinados, ya que sus puntuaciones estarán basadas en un modelo que no representa adecuadamente la relación entre la habilidad y la probabilidad de respuesta correcta. Por lo tanto, es importante evaluar cuidadosamente el ajuste del CCI al modelo IRT antes de utilizar e interpretar los parámetros de los ítems y las estimaciones de habilidad. Un mal ajuste puede comprometer la validez y la confiabilidad de las mediciones realizadas con el test.

Extensiones y modelos alternativos para la CCI

Si bien los modelos básicos de la Teoría de Respuesta al Ítem (IRT) son ampliamente utilizados, existen diversas extensiones y modelos alternativos que han sido propuestos para abordar situaciones más complejas o relajar algunos de los supuestos subyacentes. Estas extensiones permiten una representación más precisa de la relación entre la habilidad latente y la probabilidad de respuesta correcta en diferentes contextos de medición.

Modelos politómicos para ítems con respuestas graduadas: Muchos instrumentos de medición utilizan ítems con respuestas graduadas u ordenadas, como escalas Likert (De Ayala, 2009). Para estos casos, se han desarrollado modelos politómicos que extienden el CCI para ítems con más de dos categorías de respuesta. Algunos ejemplos son el Modelo de Respuesta Graduada (Samejima, 1969) y el Modelo de Crédito Parcial (Masters, 1982).

Interpretación de la Gráfica:

• Dimensión Latente: El eje horizontal representa la dimensión latente o nivel de habilidad (en este caso, podría interpretarse como nivel de autoestima). A medida que se avanza hacia la derecha en este eje, se incrementa el nivel de autoestima del individuo.
• Probabilidad de Resolución: El eje vertical muestra la probabilidad de resolver el ítem en una categoría específica. Esto se traduce en la probabilidad de que un individuo con un determinado nivel de autoestima seleccione una de las categorías de respuesta disponibles.

Ítem 1: “Me siento seguro(a) de mí mismo(a) en la mayoría de las situaciones.”

Curvas de Categoría: Cada curva representa una categoría de respuesta diferente en la escala Likert (por ejemplo, 1 = “Totalmente en desacuerdo”, 2 = “En desacuerdo”, 3 = “De acuerdo”, 4 = “Totalmente de acuerdo”).

Categoría 0 (Negro): Corresponde a la categoría con menor puntaje, por ejemplo, “Totalmente en desacuerdo”. La probabilidad de seleccionar esta categoría es mayor en personas con baja autoestima, disminuyendo a medida que el nivel de autoestima aumenta.

Categoría 1 (Rojo): Representa una categoría intermedia, como “En desacuerdo”. Esta curva indica que personas con un nivel de autoestima ligeramente bajo tienen más probabilidades de elegir esta opción.

Categoría 2 (Verde): También una categoría intermedia, por ejemplo, “De acuerdo”. Aquí, la probabilidad de seleccionar esta opción es mayor en individuos con autoestima media.

Categoría 3 (Azul): Esta última categoría podría ser “Totalmente de acuerdo”. Es más probable que sea seleccionada por personas con un alto nivel de autoestima.

Aplicaciones del Modelo de Respuesta Graduada en la Evaluación de Autoestima:

• Analiza la probabilidad de selección de cada categoría de respuesta según el nivel de autoestima.
• Identifica puntos de transición entre categorías de respuesta o establece en qué niveles de autoestima es más probable que una persona pase de “En desacuerdo” a “De acuerdo”.
• Evalúa la diferenciación entre categorías de la escala Likert o determinar si las respuestas de la escala están bien diferenciadas.
• Permite comparar la autoestima entre diferentes grupos demográficos.
• Facilita el desarrollo de guías interpretativas para profesionales.

Modelos multidimensionales para constructos complejos: Los modelos IRT unidimensionales asumen que una sola habilidad latente influye en las respuestas a los ítems. Sin embargo, en muchas áreas, los constructos medidos son complejos y multidimensionales (Reckase, 2009).

Los modelos multidimensionales de IRT permiten representar estas situaciones, modelando las interacciones entre múltiples habilidades latentes y las respuestas a los ítems. En estos modelos, el CCI se extiende a una superficie multidimensional que describe la probabilidad de respuesta correcta en función de múltiples habilidades.

Por ejemplo, consideremos una evaluación integral de competencias en el área de ciencias para estudiantes de secundaria. Esta evaluación busca medir simultáneamente tres dimensiones: conocimiento científico, razonamiento científico y habilidades prácticas de laboratorio.

Aplicación del modelo IRT multidimensional:

• Diseño del test: Se crean ítems que requieren la aplicación de múltiples habilidades. Por ejemplo, un ítem podría presentar los resultados de un experimento y pedir al estudiante que interprete los datos (razonamiento), identifique el concepto científico relevante (conocimiento) y sugiera mejoras en el diseño experimental (habilidades prácticas).
• Análisis de ítems: El modelo multidimensional permite evaluar cómo cada ítem se relaciona con las tres dimensiones. Algunos ítems pueden cargar fuertemente en una dimensión, mientras que otros pueden requerir una combinación de habilidades.
• Perfiles de habilidad: En lugar de una única puntuación, cada estudiante recibe un perfil tridimensional que muestra sus niveles en conocimiento, razonamiento y habilidades prácticas.
• Diagnóstico detallado: Los educadores pueden identificar patrones específicos de fortalezas y debilidades. Por ejemplo, un estudiante podría tener un alto conocimiento científico, pero dificultades en el razonamiento aplicado.
• Planificación curricular: Los resultados pueden informar sobre qué aspectos del plan de estudios necesitan más atención, permitiendo un enfoque equilibrado en las tres dimensiones.
• Evaluación de programas: A nivel escolar o distrital, se puede analizar cómo diferentes enfoques educativos impactan en las tres dimensiones, permitiendo una evaluación más completa de la efectividad de los programas de ciencias.

Este enfoque multidimensional proporciona una comprensión más rica y matizada de las competencias científicas de los estudiantes, superando las limitaciones de una puntuación única y permitiendo intervenciones educativas más precisas y personalizadas.

Modelos de respuesta al ítem no paramétricos: Los modelos IRT paramétricos, como los de 1, 2 y 3 parámetros, imponen formas funcionales específicas en el CCI. Sin embargo, los modelos no paramétricos relajan estos supuestos y estiman el CCI directamente a partir de los datos, sin imponer una forma funcional predeterminada (Woods & Thissen, 2006).

Estos enfoques no paramétricos pueden ser útiles cuando los supuestos de los modelos paramétricos no se cumplen o cuando se desea explorar formas alternativas del CCI. Algunos ejemplos son los modelos de kernel suavizado y los modelos aditivos generalizados.

Herramientas y software:

• R package ltm para modelamiento IRT y cálculo de CCI
• jMetrik para análisis de CCI y CCT con interfaz gráfica
• Guía de uso de IRTPRO para estimación de parámetros y visualización

Bibliografía

Attorresi, H. F., Lozzia, G. S., Abal, F. J. P., Galibert, M. S., & Aguerri, M. E. (2009). Teoría de Respuesta al Ítem. Conceptos básicos y aplicaciones para la medición de constructos psicológicos. Revista Argentina de Clínica Psicológica, 18(2), 179-188. https://www.redalyc.org/pdf/2819/281921792007.pdf

Baker, F. B. (2001). The Basics of Item Response Theory. ERIC. https://edres.org/irt/baker/final.pdf

Bond, T. G., & Fox, C. M. (2015). Applying the Rasch Model: Fundamental Measurement in the Human Sciences (3rd ed.). Routledge. https://doi.org/10.4324/9781315814698

Camilli, G., & Shepard, L. A. (1994). Methods for Identifying Biased Test Items. Sage Publications. https://www.academia.edu/48120028/Methods_for_identifying_biased_test_items

De Ayala, R. J. (2009). The Theory and Practice of Item Response Theory. Guilford Publications. https://archive.org/details/theorypracticeof0000deay

Embretson, S. E., & Reise, S. P. (2000). Item response theory for psychologists. Lawrence Erlbaum Associates Publishers. https://doi.org/10.4324/9781410605269

Fan, X. (1998). Item response theory and classical test theory: An empirical comparison of their item/person statistics. Educational and Psychological Measurement, 58(3), 357-381. https://doi.org/10.1177/0013164498058003001

López-Cuadrado, J. (2008). Ejemplo de CCI según el modelo de tres parámetros. Evaluación mediante test adaptativos informatizados en el contexto de un sistema adaptativo para el aprendizaje de la Lengua Vasca. Recuperado de – Ejemplo de CCI según el modelo de tres parámetros.   | Download Scientific Diagram (researchgate.net)

Hambleton, R. K., & Swaminathan, H. (2010). Item Response Theory: Principles and Applications. Springer Science & Business Media. https://doi.org/10.1007/978-94-017-1988-9

Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of Item Response Theory. Sage. https://www.jstor.org/stable/1435166

Haladyna, T. M., & Rodriguez, M. C. (2013). Developing and Validating Test Items. Routledge. https://doi.org/10.4324/9780203850381

Kolen, M. J., & Brennan, R. L. (2014). Test Equating, Scaling, and Linking: Methods and Practices. Springer. https://doi.org/10.1007/978-1-4939-0317-7

Masters, G. N. (1982). A Rasch model for partial credit scoring. Psychometrika, 47(2), 149-174. https://doi.org/10.1007/BF02296272

Reckase, M. D. (2009). Multidimensional item response theory. Springer. https://doi.org/10.1007/978-0-387-89976-3

Smith, M.L. (2022). The State of Educational Assessment. Journal of Testing and Evaluation, 44(11), 2205-2219.

Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometrika monograph supplement, 34(4, Pt. 2). https://www.psychometricsociety.org/sites/main/files/file-attachments/mn17.pdf

Valdés Veloz, H., Olivier, Y., & Mercedes, N. (2014). Introducción a la teoría de respuestas al ítem. Instituto Dominicano de Evaluación e Investigación de la Calidad Educativa (IDEICE). ISBN: 978-9945-8859-8-9. https://ideice.gob.do/pdf/publications/20171130164526.pdf

Wright, B. D., & Stone, M. H. (1979). Best test design. MESA Press. https://archive.org/details/1979-wright-and-stone-best-test-design/page/n9/mode/2up

Woods, C.M., Thissen, D. (2006). Item Response Theory with Estimation of the Latent Population Distribution Using Spline-Based Densities. Psychometrika 71, 281–301. https://doi.org/10.1007/s11336-004-1175-8

Wim J. Linden, Gees A.W. Glas. (2000). Computerized Adaptive Testing: Theory and Practice. Kluwer Academic Publishers. https://doi.org/10.1007/0-306-47531-6