Correlación y regresión simple

.

Por: Aylen Zarhek Gutiérrez Nova

¿Cómo y cuándo hacer una correlación o regresión simple? – Ejemplo en JASP

Como parte de la investigación en psicología se suelen emplear métodos estadísticos que nos permiten describir y realizar inferencias sobre una población. Dos de los métodos más empleados a la hora de estudiar la relación entre dos variables, son la correlación y la regresión simple.

La correlación resulta útil cuando queremos estimar si existe relación entre dos o más variables, así cómo las características de la misma. De encontrarse que están correlacionadas podemos proceder a realizar un modelo de regresión. Por su parte, la regresión es probablemente la técnica estadística más importante, ya que nos permite explicar un fenómeno y predecirlo, además de obtener información sobre la influencia de una variable independiente sobre una dependiente (Pérez-Tejada, 2008).

A continuación, detallaremos sus definiciones, haremos una distinción entre ellos y revisaremos brevemente cómo realizar estos análisis en el programa JASP a través de un ejemplo.

¿Qué es una correlación?

Antes de hacer una regresión, necesitamos conocer el coeficiente de correlación. Este es un parámetro que indica el grado de relación simultáneo entre dos variables. La correlación se ocupa de establecer la dirección, la forma y la magnitud de la relación entre dos variables. La dirección es indicada por el signo, que puede ser positivo o negativo; la forma, puede ser lineal o curvilínea; mientras que la magnitud refiere al grado o fuerza de la relación, o tamaño del efecto (Betanzos et al., 2017; Hernández-Sampieri, 2018; Pérez-Tejada, 2008).

Interpretación

Los coeficientes de correlación comprenden valores entre el -1 y el +1. Así, dependiendo de su valor, tendrán un significado u otro. En primer lugar, si el signo de la correlación es positivo, significa que cuando una variable crece la otra también lo hace. Por su parte, cuando el signo es negativo, la correlación es inversa, y a medida que una variable aumenta, la otra disminuye (Clark-Carter, 2002).

Cuando la relación es perfecta, igual a -1 o +1, la correlación es máxima y podemos predecir con exactitud una variable a partir de la otra. En esta situación, cuando X cambia también Y presenta un cambio. Todos los puntos están sobre una línea recta si la relación es lineal.

Cuando la relación es inexistente, igual a 0, la correlación alcanza su mínimo, y el hecho de conocer el valor de una de las variables no ayuda en nada a predecir el valor de la otra.

Las relaciones imperfectas tienen niveles intermedios de correlación, distintos a cero, y la predicción es aproximada. En este caso, el mismo valor de X no siempre conduce al mismo valor de Y. Sin embargo, en promedio, Y cambia de manera sistemática con X, y podemos lograr una predicción mejor de Y si conocemos el valor de X que si no lo conocemos (Pagano, 2008).

Si tenemos pares de datos (x, y) y vemos que la dispersión sigue la forma lineal, podemos resumir estos datos con el promedio de las X, las desviaciones estándar de las X (S_X), el promedio de las Y, las desviaciones estándar de las Y (S_y), y, finalmente, el coeficiente de correlación. Si la forma de dispersión es lineal, una buena medida de la fuerza es el coeficiente de correlación, r de Pearson (Mendenhall et al., 2010; Pagano, 2008).

¿Qué es una regresión simple?

Una regresión lineal es un modelo estadístico que permite explicar la relación lineal entre dos o más variables. Está asociado con el coeficiente de correlación r de Pearson, y representa una extensión de este (Hernández-Sampieri, 2018).

En el caso específico de la regresión simple, el modelo permite predecir el valor de una variable dependiente y, basados en el valor de una variable independiente x, a través de la ecuación de la recta que mejor describe la relación. Esta ecuación representa la línea que mejor se ajusta a los puntos en un gráfico de dispersión (Carrasquilla-Batista et al., 2016).

Es preciso señalar que cuando trazamos estos pares de variables (X, Y), usamos la convención de que, la variable dependiente o respuesta se identifica como Y, en tanto que la variable independiente o predictora se identifica como X.

¿En qué se diferencian?

La correlación y la regresión están muy relacionadas entre sí. Ambas implican la relación entre dos o más variables. Sin embargo, su principal diferencia radica en el tipo de hipótesis que permiten probar.

La correlación sirve principalmente para averiguar la relación de las variables, en términos de magnitud y dirección, sin asumir una relación de causalidad entre estas (Pagano, 2008). Por otro lado, la regresión utiliza esta relación para hacer una predicción. Al definir una variable como predictora y otra como de respuesta en la regresión, la dirección causal ya está dada. Así, si existe una relación causal entre dos variables, un análisis de regresión puede predecir una variable con la otra, y generalizar este resultado. Entre mayor sea la correlación entre las variables (covariación), mayor es la capacidad de predicción que podemos realizar (Hernández-Sampieri, 2018; Pérez-Tejada, 2008).

Con todo esto, es importante tener en mente que la regresión por sí misma no implica una causalidad, puesto que para definir la dirección entre variables, esta primero debe contar con un sustento teórico sólido. Así, no se puede “buscar” la causalidad con la regresión, sino que este método sólo puede utilizarse si se asume una relación causal (Hernández–Sampieri, 2018).

¿En qué casos se calcula o cuándo es apropiado hacerlo?

Correlación. Se calcula cuando estamos interesados únicamente en investigar la posible existencia de una relación entre dos variables.

Cuando las variables son de intervalos o razón se utiliza el coeficiente de correlación de Pearson. Con variables ordinales de múltiples rangos, utilizaremos los coeficientes Kendall y Spearman y en el caso de variables nominales u ordinales la Chi-cuadrada. El coeficiente de correlación más ampliamente utilizado, es el coeficiente r de Pearson (Hernández-Sampieri, 2018).

Regresión lineal simple. Se calcula cuando existen relaciones lineales entre variables, es importante revisar los valores atípicos, ya que la regresión lineal es sensible a sus efectos. No es útil cuando la relación entre variables es curvilínea, es decir, aquellas relaciones en las que la tendencia varía, siendo primero ascendente y luego descendente, o viceversa (Hernández-Sampieri, 2018).

Se debe tener en cuenta que la regresión lineal simple se fundamenta en otros supuestos: la independencia y normalidad de las variables. Del mismo modo, se espera que haya homogeneidad de la varianza de los residuos. En el caso de la regresión lineal múltiple, también es importante considerar la multicolinealidad, que ocurre cuando las variables independientes están altamente correlacionadas entre sí (Carrasquilla-Batista et al., 2016; Goss-Sampson y Meneses, 2019).

Es importante tener en cuenta estos supuestos al realizar un análisis de regresión lineal, ya que de no cumplirse  la validez de los resultados y las conclusiones que se puedan extraer pueden verse afectadas.

Ejemplo

La Escala de Wechsler de Inteligencia para Adultos (WAIS), es una prueba estandarizada que se usa para medir el coeficiente intelectual de las personas adultas. Las puntuaciones se agrupan en siete categorías.  Puntuaciones por debajo de 69 indican un nivel muy bajo, entre 90 y 109 puntos indican un nivel medio, y puntuaciones superiores a 130 indican un nivel muy superior.

En una muestra de 25 estudiantes de una universidad, se aplica el WAIS y se obtiene además, el promedio de sus calificaciones del semestre anterior. A partir de estos datos y utilizando el programa JASP, calcularemos el coeficiente de correlación entre ambas variables, y realizaremos una regresión lineal.

Para realizar la regresión lineal, tomaremos el CI como variable independiente (x), y el promedio de las calificaciones como variable dependiente (y), ya que teóricamente estas dos variables están relacionadas entre sí. En este sentido, se espera que, personas con un CI más alto obtengan calificaciones más altas y viceversa.

Pasos. Correlación lineal.

1. Abrir el archivo con nuestros datos, que previamente debió ser guardado en formato separado por comas (.csv).

(Menú Principal. Abrir. Ordenador. Buscar. Nombre del archivo. Abrir).

1. A continuación, verificamos que la escala de las variables se encuentre correctamente, y realizamos cambios de ser necesarios.

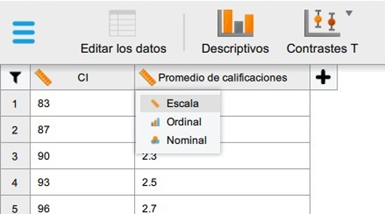
1. Damos clic en la opción Regresión del menú superior. Luego, en el apartado clásico, damos clic en correlación.

Ubicamos nuestras variables en la caja de asignación. Y tras esto, hacemos una revisión del supuesto de normalidad.

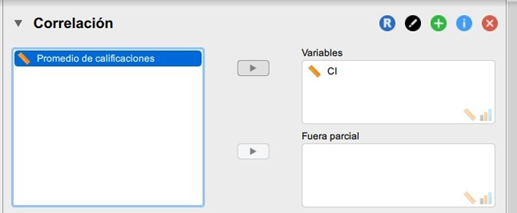
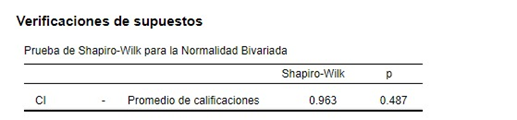
Como el valor-p en este caso (0.487) es mayor a alfa (0,05), se acepta la hipótesis de que los datos siguen una distribución normal. Por lo tanto, concluimos que las variables presentan un comportamiento normal o paramétrico.

1. De acuerdo con el resultado de la prueba de normalidad, seleccionamos el Coeficiente de Correlación Muestral que se ajuste a nuestro caso. En nuestro ejemplo, las variables cumplen los supuestos de la prueba paramétrica, r de Pearson, por ende utilizaremos este coeficiente. Este coeficiente de correlación es útil para relaciones lineales, pero no para relaciones curvilíneas en cuyo caso o cuando las variables son ordinales se debe utilizar el coeficiente rho de Spearman.

Continuamos, seleccionando la dirección de nuestra hipótesis alterna. En Opciones Adicionales, seleccionamos Reportar la significancia, Marcar relaciones significativas, e Intervalos de confianza. Para finalizar, activamos los Gráficos de dispersión.

Interpretación de resultados.

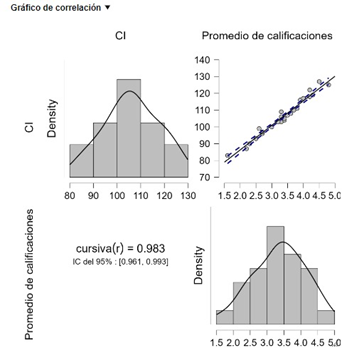
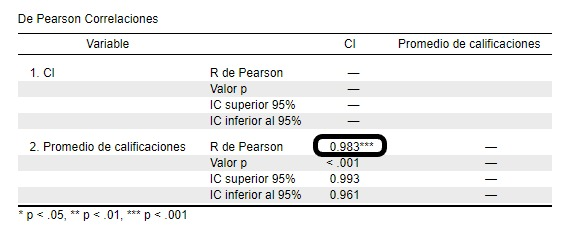
El valor del coeficiente r de Pearson (0.983), representa una relación positiva entre las variables. Además, su valor es cercano a 1, lo cual también indica una fuerte correlación entre ambas variables. A medida que el CI aumenta, el promedio de las calificaciones del estudiante también lo hace.

El intervalo de confianza de 95% oscila de 0.993 a 0.961. Adicionalmente, encontramos que el valor de r es estadísticamente significativo (valor-p < 0.001). Con esto, podemos concluir que existe una relación lineal significativa entre ambas variables. Y podemos realizar una regresión lineal.

Regresión lineal simple. Para realizar el análisis de regresión lineal, volveremos a dar clic en la opción Regresión del menú superior. Luego, en el apartado clásico, damos clic en regresión lineal.

Ubicamos nuevamente nuestras variables en la caja de asignación, sólo que en este caso haremos la distinción entre variable dependiente (promedio de las calificaciones), y la variable independiente (CI).

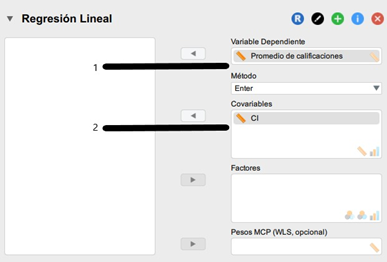
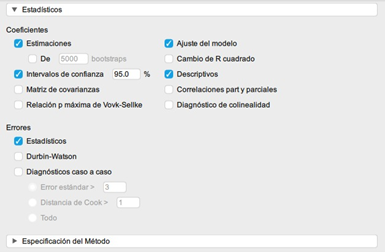
Marcamos las siguientes opciones en los estadísticos, e inspeccionamos sus valores en las tablas que nos proporciona JASP para verificar que se estén cumpliendo los supuestos. Es muy importante no olvidar los estadísticos residuales de la regresión.

La tabla Resumen del Modelo muestra que la correlación (R de pearson) entre las dos variables es alta (0,983). El valor R² (0,966) indica que el Coeficiente Intelectual representa el 96,6% de la varianza en el promedio de las calificaciones. La prueba Durbin-Watson comprueba las correlaciones entre los residuos, lo que podría invalidar el test. Debería estar por encima de 1 y por debajo de 3, idealmente cerca de 2.

La tabla ANOVA muestra todas las sumas de los cuadrados antes mencionados. “Regresión” es el modelo y “Error” el residual. El estadístico F es significativo p = >0,001. Esto nos dice que la regresión entre las dos variables es significativa.

Esta tabla proporciona los coeficientes no estandarizados que pueden introducirse en la ecuación lineal para realizar predicciones.

y = c + b*x

y. Puntuación estimada de la variable dependiente resultado.

c. Constante

b. Coeficiente de regresión (“CI”).

x. Puntuación en la variable predictiva independiente.

Por ejemplo, para una persona con un CI de 96, el promedio de sus calificaciones se puede predecir con la siguiente fórmula:
Prom. Calificaciones = -3.656 + (0.066 * 96) = 2.68

Si analizamos nuestros datos, encontramos que este resultado es bastante cercano al promedio de las calificaciones del semestre anterior de esta persona.

1. Finalmente, seleccionamos las gráficas de residuales, y verificamos que no se estén incumpliendo los supuestos de normalidad, y varianza constante.

Para que se cumpla el supuesto de normalidad, los puntos deben acercarse a la recta lo más posible en el “Gráfico Q-Q de los Errores Tipificados”. En el gráfico “Errores vs. Predicho”, debemos revisar que la nube de puntos, no siga algún patrón de cono o embudo, esto indicaría que no se está violando el supuesto de varianza constante, o homocedasticidad.

REFERENCIAS

Betanzos, F. G., y López, J. K. C. (2017). Estadística aplicada en psicología y ciencias de la salud. Editorial El Manual Moderno.

Carrasquilla-Batista, A., Chacón-Rodríguez, A., Núñez-Montero, K., Gómez-Espinoza, O., Valverde, J., y Guerrero-Barrantes, M. (2016). Regresión lineal simple y múltiple: aplicación en la predicción de variables naturales relacionadas con el crecimiento microalgal. Revista Tecnología en Marcha, 29, 33-45.

Clark-Carter, D. (2002). Investigación cuantitativa en psicología: del diseño experimental al reporte de investigación. Oxford University Press.

Goss-Sampson, M. A., y Meneses, J. (2019). Análisis estadístico con JASP: Una guía para estudiantes.

Hernández-Sampieri, R. (2018). Metodología de la investigación: las rutas cuantitativa, cualitativa y mixta. McGraw Hill México

Mendenhall, W., Beaver, R. J., y Beaver, B. M. (2010). Introducción a la probabilidad y estadística. 13ª. Edición. México: Cengage Learning.

Pagano, R. (2008). Estadística para las ciencias del comportamiento y de la salud. México: Thomson.

Pérez-Tejada, H. (2008). Estadística para las ciencias sociales, del comportamiento y de la salud. Cengage learning. 3ª. Edición. México: Cengage Learning.